Trygonometria Piotruś: Wykaż, że jeśli α jest kątem ostrym i 2cos²α + 5sin²α=4 to (tgα +ctgα)²=4,5 Proszę o pomoc.

Piotruś: Nieaktualne. Udało mi się to zrobić.

Saizou : 2cos²x+5sin²x=4 2(1−sin²x)+5sin²x=4 2−2sin²x+5sin²x=4 3sin²x=2

	2
sin2x=
	3

2cos²x+5(1−cos²x)=4 2cos²x+5−5cos²x=4 −3cos²x=−1

	1
cos2x=
	3

(tgx+ctgx)²=tg²x+2tgx*ctgx+ctg²x

	sin2x		2   3		2
tg2x=		=		=		=2
	cos2x		1   3		1

	cos2x		1   3		1
ctg2x=		=		=
	sin2x		2   3		2

tgx*ctgx=1

	1		1
zatem (tgx+ctgx)2=2+2*1+		=4
	2		2

Nienor:

	1		tg2α+1
T:tg2α+2tgαctgα+ctg2α=tg2α+2+		=2+		=
	tg2α		tg2α

	sin2α   +1 cos2α		sin2α+cos2α   cos2α
2+		=2+		=
	sin2α   cos2α		sin2α   cos2α

	1   cos2α		1
2+		=2+
	sin2α   cos2α		sin2α

Z założenia: 2(1−sin²α)+5sin²α=4 2+3sin²α=4 3sin²α=2

	2
sin2α=
	3

1		3
	=
sin2α		2

T: 2+1,5=3,5 Albo jest gdzieś błąd w przekształceniach, schowany gdzieś niecnie, albo źle przepisałeś zadanie. Tak czy sia, takie obliczenia w trygonometrii polegają na czymś podobnym do tego powyżej.

Nienor: A już widzę, co mam źle. Sprowadzani do wspólnego mianowinika. Ma być:

tg4α+1
	i nici z przekształcenia
tg2α

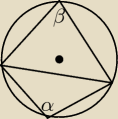
Piotruś: Dzięki za pomoc. Mam pytanie odnośnie tego. α=120 Da się wyznaczyć β?

Saizou : Czworokąt można wpisać w okrąg jeżeli sumy przeciwległych kątów są równe 180, zatem α+β=180 120+β=180 β=60