Dany jest trójkąt ABC, w którym kąt ACB = 90 stopni.
erytrocyt: Dany jest trójkąt ABC, w którym kąt ACB = 90 stopni. Oblicz wysokość tego trójkąta poprowadzoną
z wierzchołka C, jeżeli |AC|=6 cm i środkowa |CE| ma długość 5 cm
17 maj 22:39
Mila:
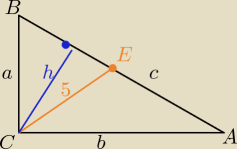
|AC|=6
|CE|=|AE|=|BE|=5⇔
|AB|=c=10
a
2=10
2−6
2
a=8
| | 1 | | 1 | |
PΔ= |
| a*b⇔PΔ= |
| *6*8=24 |
| | 2 | | 2 | |
5h=24 dokończ
17 maj 22:52
Eta:
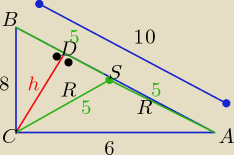
|AB|=2R =10 −−− długość średnicy okręgu opisanego na trójkącie
| | 8*6 | | 10*h | |
P= |
| = 24 i P= |
| =5h |
| | 2 | | 2 | |
to: 5h=24 ⇒ h=........
17 maj 22:53
erytrocyt: @mila
czemu CE jest równe AE?
18 maj 12:20
Kaja: bo zarówno Ce jak i Ae są promieniami okręgu opisanego na tym trójkącie
18 maj 12:22
Mila:
Środek okręgu opisanego na Δ prostokątnym leży w środku przeciwprostokatnej.
Srodkowa CE jest promieniem okręgu opisanego na tym trójkacie.
18 maj 15:32
 |AC|=6
|CE|=|AE|=|BE|=5⇔
|AB|=c=10
a2=102−62
a=8
|AC|=6
|CE|=|AE|=|BE|=5⇔
|AB|=c=10
a2=102−62
a=8
 |AB|=2R =10 −−− długość średnicy okręgu opisanego na trójkącie
|AB|=2R =10 −−− długość średnicy okręgu opisanego na trójkącie