Trygonometria Równina: Proszę o pomoc Określ zb.wart. i naszkicuj wykres funkcji f: D→R, jeżeli: i) D=<π;π>\{^−π₂; ^π₂}, f(x)=cosx*√1+tg²x Wytłumaczcie, jak dojść do tego, żeby łatwo było narysować

Równina: Proszę

Bogdan:

	cos2x		sin2x		1
a = 1 + tg2x =		+		=
	cos2x		cos2x		cos2x

w mianowniku jest cos²x

	1
√a =
	|cosx|

	cosx
f(x) =
	|cosx|

Równina: Ok, mam jeszcze pytanie: najpierw rysuje cosx, później obliczam z |cosx| pierwszy i drugi przypadek i rysuje, tak?

Bogdan: Nie potrzeba rysować wykresu y = cosx, trzeba jednak wiedzieć, że:

	π		π
cosx < 0 dla x ∊ <−π, −		)∪(		), π>
	2		2

	π		π
cosx > 0 dla x ∊ (−		,		)
	2		2

Równina: Ok, dzięki

Bogdan:

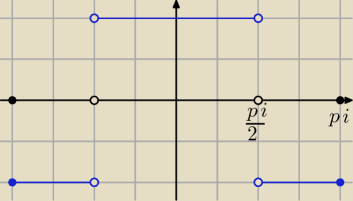
	π		π
f(x) = −1 dla x∊<−π, −		)∪(		, π>
	2		2

	π		π
f(x) = 1 dla x∊(−		,		)
	2		2

Podaj zbiór wartości funkcji f(x)

Równina: Zb.wart.=<−1;1)

Równina: tak?

Bogdan: Nie

asdf:

	cos0
równina, ile jest		?
	|cos0|

Bogdan: dokończ zapis ZW_f: y∊...

Równina: asdf: 0 Zw:= −1

Równina: asdf: 1

Bogdan: źle,

asdf: podpowiem:

cos(π)		−1		−1
	=		=		= −1
|cos(π)		|−1|		1

cos(0)		1		1
	=		=		= 1
|cos(0)		|1|		1

więc?..juz masz prawie gotowca

asdf: −1 i 1 nie są granicami tylko wartościami, ktore ograniczają tą funkcję. Trzeba zwrócić uwagę na nawiasy.

Równina: zb.wart.=<1>suma (1) nie wiem

asdf: co ty kombinujesz? odp: <−1;1>

Równina: napisałam wcześniej <−1;1) tylko dlaczego dla calej 1, jak są zbiory otwarte

Równina: utrudniam sobie życie

asdf: jakie otwarte?! przeciez to chodzi o zbior argumentow ktore wykluczasz, a funkcja przyjmuje wartość:

	π		π
y = 1 dla x∊ (−		;		)
	2		2

	π		π
y = −1 dla x ∊<π;−		) ∪ (		;π>
	2		2

asdf: po 2) nie ma takiego czegos ja zbior otwarty − a przynajmniej na razie wiedza o tych zbiorach jest Ci nie potrzebna..to PRZEDZIAŁ JEST OTWARTY ALBO DOMKNIĘTY

Bogdan: Ciągle nikt nie podał zbioru wartości funkcji w postaci ZW = ..., względnie ZW: y∊...

asdf: oj Bogdan...czepiasz sie

Bogdan: Nie czepiam się, należy poprawnie zapisać ZW = ... albo chociaż y∊...

Równina: Dobrze, już rozumiem o co chodzi Dziekuję bardzo za tłumaczenie

Bogdan: Dobrze, że dziękujesz, podaj jednak zbiór wartości funkcji, chyba, że nie potrafisz, to Ci podam

Równina: Zw=<−1;1>

Równina: tak ja asdf pisał

asdf: przeciez napisalem w 14:49

asdf: @rownina nie <−1;1> tylko to co z 14:49 ZWF = {−1,1} (zbior dwuelementowy)

Bogdan: To jest Równina zła odpowiedź,

Bogdan: O, teraz asdf podał poprawnie

Równina: co ty kombinujesz? odp: <−1;1> a to do czego było

Bogdan: Zbiór <−1, 1> nie jest zbiorem wartości omawianej funkcji

Równina: ok

pigor: ..., no to jeszcze ja podsumuję 1−sze zadanie np. tak : y= cos²x√1+tg²x ⇒ y²=cos²x*(1+tg²x) ⇔ y²= cos²x+sin²x ⇔ y²=1 ⇔ ⇔ |y|=1 ⇔ y=−1 lub y=1 ⇒ y∊{1,−1} − szukany zbiór wartości funkcji f , a z określoności y=tgx wykres funkcji f "wygląda" na <−π ; π> tak { 1 tam gdzie cosx >0 ; f(x)= { nie istnieje dla cosx=0 ⇔ x= ¹₂π . ... {−1 tam gdzie cosx<0 ;