 W trójkąt równoramienny ABC o ramionach długości 10 cm i podstawie 12 cm wpisano
trójkąt równoramienny KLM tak, że jego wierzchołek M leży w środku podstawy AB trójkąta ABC,
zaś podstawa KL jest równoległa do AB. Jakie wymiary musi mieć trójkąt KLM, aby jego pole było
największe?
Nie wiem jak zabrać sie do tego zadania. Myślę że szkic powinien wyglądać tak:
W trójkąt równoramienny ABC o ramionach długości 10 cm i podstawie 12 cm wpisano
trójkąt równoramienny KLM tak, że jego wierzchołek M leży w środku podstawy AB trójkąta ABC,
zaś podstawa KL jest równoległa do AB. Jakie wymiary musi mieć trójkąt KLM, aby jego pole było
największe?
Nie wiem jak zabrać sie do tego zadania. Myślę że szkic powinien wyglądać tak:
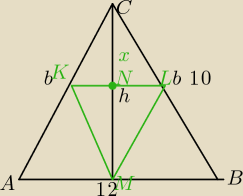 h2=102−62
h=8
ΔKLC∼ΔABC⇔
h2=102−62
h=8
ΔKLC∼ΔABC⇔
| x | h | x | 8 | ||||
= | ⇔ | = | ⇔ | ||||
| KL | AB | KL | 10 |
| 5 | ||
KL= | x | |
| 4 |
| 1 | ||
PΔKLM= | |KL|*(h−x)⇔ | |
| 2 |
| 5 | 5 | |||
PΔKLM= | x*(8−x)= | (8x−x2) funkcja ma wartość największą w wierzchołku paraboli | ||
| 8 | 8 |
| −8 | ||
xw= | =4 | |
| −2 |
| 5 | ||
KL= | *4=5 | |
| 4 |