Funkcja
bezendu: Uzasadnij, że dla każdej liczby naturalnej n suma f(n)+f(n+1)+f(n+2)+f(n+3) ma stała wartość
wiem, że są to 4 kolejne liczby naturalne z czego przynajmniej jedna jest parzysta i jedna
podzielna przez 3...
16 maj 11:17
aniabb: a jaka to funkcja?
16 maj 11:18
bezendu: Funkcja f każdej liczbie rzeczywistej x przyporządkowuje najmniejszą liczbę ujemną a taką że
x+a jest liczbą całkowitą podzielną przez 4
16 maj 11:20
Fan ETY: Niech ktoś to zrobi bo też nie rozumiem
16 maj 11:35
bezendu: Fan ETY
16 maj 11:40
aniabb: mam 2 dylematy..
czy −100 jest podzielne przez 4
i czy najmniejsza ujemna to co do wartości czy uwzględniać znak
16 maj 11:46
bezendu: najmniejszą liczbę nieujemną miało być przepraszam za pomyłkę
16 maj 11:48
aniabb:
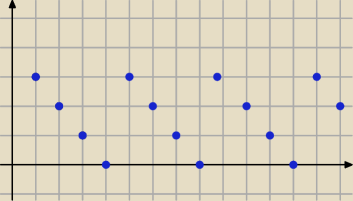
no to zdecydowanie łatwiej zatem ta funkcja wygląda tak (rys)
i jak widać jej okres wynosi 4 zatem suma dowolnych 4 jest stała i równa 6
16 maj 11:51
aniabb: miało być : suma KOLEJNYCH czterech jest stała i wynosi 6
16 maj 11:53
aniabb: jak chcecie bardziej purystyczne rozwiązanie to pewnie trzeba prosić PW
16 maj 12:01
bezendu: Dziękuje
czyli wystarczy napisać ten komentarz tylko czy lepiej zobrazować to wykresem ?
16 maj 12:03
aniabb: zdecydowanie lepiej jest narysować wykres
16 maj 12:05
bezendu: ok
16 maj 12:08
bezendu: Funkcja f każdej liczbie rzeczywistej x przyporządkowuje najmniejszą liczbę nieujemną a taką że
x+a jest liczbą całkowitą podzielną przez 4
b) Ile miejsc zerowych ma funkcja
a
1=4
a
n=100
a
2=8
r=4
4+(n−1)*4=100
4+4n−4=100
4n=100
n=25
Odp funkcja ma 25 Miejsc zerowych ∊<1,100>
16 maj 14:56
asdf: ta
16 maj 14:58
asdf: a1 = 4?
16 maj 14:59
asdf: a.. myslalem, ze chodzi o wczesniejsze zadanie z wykresem
16 maj 15:00
bezendu: nie chodzi o podpunkt b )
16 maj 15:03
bezendu: A jeszcze jedno takie pytanko jak zrobić to innym sposobem
zadanie jest ze zbioru Kiełbasy i
tam na początku tego zbioru widnieje ''zbiór zadań z danego działu nie wymaga wiedzy z działu
następnego'' więc można to chyba jakoś zrobić inaczej
16 maj 15:06
bezendu:
16 maj 15:45
Basia:
spośród liczb n, n+1, n+2, n+3 gdzie n∊N dokładnie jedna jest podzielna przez 4
możesz kolejno rozważać przypadki:
1. n jest podzielna przez 4
wtedy
f(n) = 0
f(n+1) = 3
f(n+2) = 2
f(n+3) = 1
f(n)+f(n+1)+f(n+2)+f(n+3) = 0+3+2+1=6
2. n+1 jest podzielna przez 4
wtedy
f(n) = 1
f(n+1) = 0
f(n+2) = 3
f(n+3) = 2
f(n)+f(n+1)+f(n+2)+f(n+3) = 1+0+3+2=6
pozostałe dwa przypadki rozważ sam
16 maj 18:00
bezendu: Ok, dziękuje za odpowiedź
16 maj 18:02
Krzysiek : Widze ze mamy przyszlorocznego maturzyste
16 maj 22:20
Mila: I ambitnego,Krzysiu.
16 maj 23:11
Eta:
16 maj 23:12