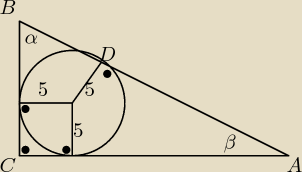
Pola trójkątów Julia: W trójkącie prostokątnym ABC cosinus kąta ABC wynosi 0,8. W trójkąt wpisano okrąg; punkt D jest punktem styczności tego okręgu z przeciwprostokątną AB. Wiedząc, że promień tego okręgu jest równy 5 cm, oblicz pola trójkątów ADC i DBC. Proszę bardzo o pomoc w rozwiązaniu tego zadania. nie mam kompletnie pomysłu jak to zrobić

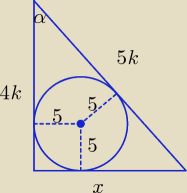Bogdan: x = √25k² − 16k² = 3k

	4k * 3k		4k + 3k + 5k
Pole P =		= 6k2 oraz P =		*5 = 30k
	2		2

6k² = 30k ⇒ k = ... dokończ