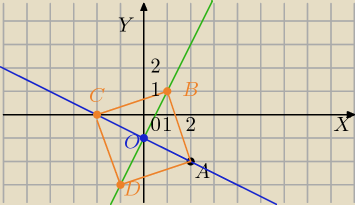
równanie prostej Kacper: Dany jest kwadrat ABCD o polu 10 i wierzchołku A (2,−2). Przekątna BD tego kwadratu ma równanie 2x−y−1=0. Oblicz współrzędne pozostałych wierzchołków kwadratu. Mam już punkt C, wyszedł mi (−2,0), ale nie wiem jak wyznaczyć B i D.

Kacper: Ma ktoś może pomysł?

Kacper: Nikt na prawdę ?

Kacper: Odświeżam. Potrzebuję to na jutro

Mila: Rozwiązuję.

Kacper: Mila, będę czekał , dzięki!

Mila: k: 2x−y−1=0. ⇔ y=2x−1 Przekątne są prostopadłe i równe AC: A=(2,−2) prosta

	−1		−1
y=		x+b i −2=		*2+b⇔−2=−1+b⇔b=−1
	2		2

AC ma równanie:

	−1
y=		x−1
	2

Punkt o− punkt przecięcia prostych

−1
	x−1=2x−1
2

x=0 i y=−1 O(0,−1) jest środkiem AC:

	xa+xc		2+xc		−1
xs=		⇔0=		⇔xc=−2 i yc=		*(−2)−1=0
	2		2		2

C=(−2,0) równanie okręgu o środku o i promieniu r=OA OA=√2²+1²=√5 x²+(y+1)²=5 i y=2x−1 x²+(2x−1+1)²=5 x²+4x²=5 5x²=5 x=1 lub x=−1 y=2*1−1=1⇔B=(1,1) lub y=2*(−1)−1=−3 ⇔D=(−1,−3)

Kacper: Dzięki!

Mila: Powodzenia na matematyce.