Zadanie dowodowe, należy wykazać stosunek pól trójkątów Licealistka: W trójkącie ABC punkty D i E dzielą bok AB na trzy równe odcinki. Punkty F i G dzielą bok BC na trzy równe odcinki, a punkt H jest środkiem boku AC. Wykaż, że PΔEGH=⁵₁₇PΔABC.

Eta:

	3a*2b*3c		18
P(ABC)=		=		, R −−− dł. promienia okręgu opisanego na trójkącie ABC
	4R		4R

	3a		2b		3c
z twierdzenia sinusów: sinα=		, sinβ=		, sinγ=
	2R		2R		2R

P(EGH)= P(ABC) −(P₁+P₂+P₃)

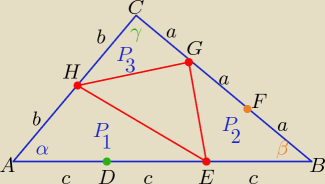
	b*2c		6abc
P1=		*sinα=
	2		4R

	2a*c		4abc
P2=		*sinβ=
	2		4R

	a*b		3abc
P3=		*sinγ=
	2		4R

	18abc		13abc		5abc
P(EGH)=		−		=
	4R		4R		4R

	5
zatem P(EGH) =		P(ABC)
	18

c.n.u Tak więc pomyliłaś się w zapisie)

Mila:

	5
PΔEGH=		PΔABC
	17

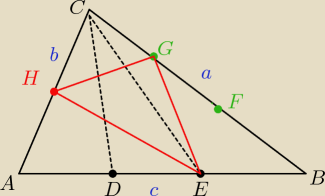
	1		1
PΔABC=		a*b*sinC lub PΔABC=		a*c*sinB lub
	2		2

	1
PΔABC=		c*b*sinA
	2

	1		1		1		1		1
PΔHGC=		*		a*		b*sinC=		*		absinC⇔
	2		3		2		2		6

	1
PΔHGC=		PΔABC
	6

	1		1		2		1		2
PGEB=		*		c**		a*sinB=		*		ac*sinB⇔
	2		3		3		2		9

	2
PGEB=		PABC
	9

	1		1		2		1		2
PHEA=		*		b*		c *sinA=		*		bcsinA⇔
	2		2		3		2		6

	2
PHEA=		PΔABC
	6

	1		2		2		3+4+6
PΔHGE=PΔABC−(		+		+		)PΔABC=(1−		)PΔABC=
	6		9		6		18

	5
PΔHGE=		PΔABC
	18

Mila: Witaj Eto, dublujemy się.Ja długo pisałam.

Eta: