monotoniczność i ekstrema gocha: Cześć, próbuję ogarnąć matmę, a orłem z niej nie jestem i już mi się wszystko pomieszało. Gdyby ktoś mi mógł pomóc rozwiązać to zadanie to byłabym bardzo, bardzo wdzięczna. Mam wyznaczyć monotoniczność i ekstrema lokalne funkcji f(x)=^x2+2_x określam tutaj dziedzina jako x>0 wyliczyłam pochodną, która wyszła mi tak: f'(x)=^x2+2_x² następnie wyznaczam przedziały monotoniczności: f'(x)>0 , f'(x)<0 x₁=− ^√2₂ x₂= ^√2₂ i teraz powinnam (co wynika z moich notatek napisać, ze funkcja rośnie w (−∞,− ^√2₂) , ^√2₂, ∞) funkcja maleje w (− ^√2₂ , ^√2₂) Fmax f(^√2₂ ) ale tu pojawiają się moje wątpliwości co do tej odpowiedzi, bo skoro dziedziną są liczby większa od zera, to Fmin nie mam, a czy te przedziały monotoniczności są dobrze określone?

Bogdan: Dziedzina D_f: x∊R \ {0}, czyli x≠0

gocha: jeden banalny błąd i zastanawiam się od godziny. Stworzyłam własną teorię, że mianownik nie może być ujemny... Dzięki bardzo za pomoc

Bogdan: Jeszcze raz ustal przedziały monotoniczności, pamiętaj, że x≠0, ustal ponownie ekstrema funkcji

gocha: jeśli chodzi o monotoniczność w przedziale, gdzie funkcja maleje, powinnam wykluczyć 0? A mógłbyś mnie naprowadzić, gdzie mam błąd jeśli chodzi o ekstrema?

Bogdan: Podaj zapis pochodnej, stosuj dużą literkę U przy zapisywaniu ułamków

gocha:

	x2+2
f(x)=
	x

	(x2+2)'(x)−(x2+2)(x)'		2x*x−(x2+2)*1		2x2−x2−2		x2−2
f'(x)=		=		=		=
	x2		x2		x2		x2

Bogdan:

	(x + √2)(x − √2)
czyli f'(x) =
	x2

gocha: aż mi wstyd za moje błędy. Jeszcze raz dzięki za pomoc

Bogdan: powodzenia

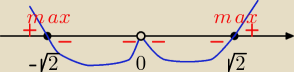
Janek191: y_min = f( √2)