Ciąg- Dowód
Piotr: Wykaż, że jeżeli długości a,b,c boków trójkąta i jego wysokość poprowadzona na bok a tworzą w
podanej kolejności ciąg geometryczny, to trójkąt jest prostokątny.
Czyli tak:
(a,b,c,h) mamy taki ciąg geometryczny
b2=ac
c2=bh
Mam udowodnić, że:
c2+b2=a2
Wg mnie wysokość jest opuszczona na najdłuższy bok. I ten ciąg geometryczny jest malejący.
Ale próbowałem dalej coś z tymi równaniami zrobić, ale do niczego konkretnego dojść nie mogę
Proszę o wskazówkę : )
15 maj 20:13
Piotr: Podbijam

15 maj 20:44
irena_1:
(a, b, c, h)− ciąg geometryczny
b=aq
c=aq
2
h=aq
3
ah=bc
sinα=1
α=90
0
15 maj 20:49
Mila:
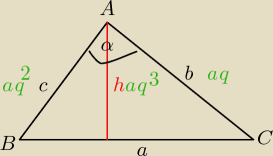
a,b,c,h− kolejne wyrazy c. geometrycznego.
q>0
| | 1 | | 1 | | 1 | |
PΔ= |
| b*c*sinα⇔PΔ= |
| *aq*aq2*sinα= |
| a2q3*sinα⇔ |
| | 2 | | 2 | | 2 | |
| 1 | | 1 | |
| a2q3*sinα= |
| a2*q3⇔ porównanie pól |
| 2 | | 2 | |
sinα=1⇔α=90
o⇔
ΔBAC jest trójkątem prostokatnym
15 maj 21:01
Piotr: Dziękuję

15 maj 21:30
Mila: 
15 maj 21:40
Piotr: A Czy sposób pani Ireny jest dobrze? Bo z góry jest założone ze jest to trojkat prostokatny. A
mi sie wydaje, ze tak nie mozna w dowodach
15 maj 21:42
irena_1:
Nie zakładałam, że trójkąt jest prostokątny.
Z warunku, że liczby tworza ciąg geometryczny, wykazałam, że
| | ah | | bc | | 1 | |
P= |
| = |
| = |
| bc sinα, czyli, że musi być sinα=1, a stąd α=900 |
| | 2 | | 2 | | 2 | |
Przeglądnij dokładnie to, co zapisałam.
15 maj 21:44
Piotr: Faktycznie

Przepraszam

Już rozumiem

15 maj 21:50

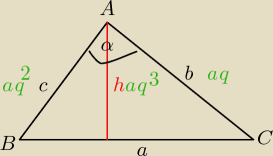 a,b,c,h− kolejne wyrazy c. geometrycznego.
q>0
a,b,c,h− kolejne wyrazy c. geometrycznego.
q>0


 Przepraszam
Przepraszam  Już rozumiem
Już rozumiem 