Wykaż, że jeśli każda z przekątnych trapezu dzieli na połowy jeden z jego kątów wajdzik: Wykaż, że jeśli każda z przekątnych trapezu dzieli na połowy jeden z jego kątów wewnętrznych, to ten trapez ma trzy równe boki. Totalnie nie mam pojęcia jak mam to wykazać.

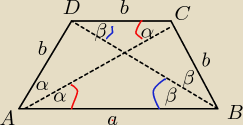
Mila: ΔACD− Δrównoramienny, kąty α (czerwony łuk) są równe jako kąty naprzemianległe wewnętrzne. AD=DC=b ΔDBC−Δrównoramienny, kąty β (niebieski łuk) są równe jako kąty naprzemianległe wewnętrzne. CB=DC=b

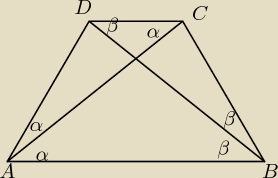
irena_1: Kąty BAC i ACD to kąty naprzemianległe, więc przystające. Kąty ABC i CAD są przystające, bo przekątna AC jest dwusieczna kąta DAB. W trójkącie ACD są dwa przystające kąty, więc jest to trójkąt równoramienny, czyli |AD|=|CD| Podobnie− trójkąt BCD jest równoramienny, czyli |CD|=|BC| Wniosek− |AD|=|CD|=|BC|

wajdzik: Dzięki dziewczyny.