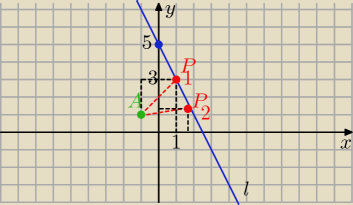
równanie prostej na płaszczyznie bangzi: Na prostej l o równaniu 2x+y=5 znajdź taki punkt P, aby jego odległość od punkty A=(−1,1) wyniosła √8 pomoże ktoś? Nie wiem jak mam sie za to zabrac

irena_1: 2x+y=5 y=−2x+5 P=(a, −2a+5) √(a+1)²+(−2a+5−1)²=√8 a²+2a+1+4a²−16a+16=8 5a²−14a+9=0 Δ=196−180=16

	14−4		14+4
a1=		=1 lub a2=		=1,8
	10		10

−2a₁+5=−2*1+5=3 lub −2*1,8+5=1,4 P₁=(1; 3) lub P₂=(1,8; 1,4)

bangzi: da to zrobić bez delty?

Eta: