Punkt S jest środkiem okręgu wpisanego w trapez ABCD (AB ∥ CD ). Wykaż, że trójk mq: Punkt S jest środkiem okręgu wpisanego w trapez ABCD (AB ∥ CD ). Wykaż, że trójkąt SBC jest prostokątny.

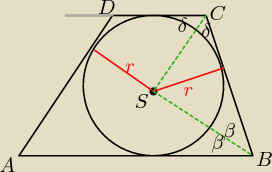
Mila: S leży na przecięciu dwusiecznych kątów wewnętrznych trapezu. 2β+2δ=180^o ( suma kątów przy ramieniu trapezu jest równa 180^o) β+δ=90^o Suma kątów w ΔCSB: ∡CSB+90⁰=180^o⇔ ∡CSB=90^o cnw

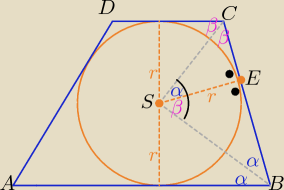
Eta: Środek S okręgu wpisanego w trapez znajduje się w punkcie przecięcia dwusiecznych SB i SC kątów trapezu 2α+2β=180^o ⇒ α+β=90^o |∡BSC|=α+β=90^o zatem trójkąt SBC jest prostokątny