Twierdzenie talesa Michał: dany jest trójkąt ABC o bokach długości AB=12, BC−8, AC=10. Poprowadzono prostą k równoległą do boku AC, która podzieliła trójkąt na dwie figury− trójkąt i trapez. Obwody tych figur są równe. Oblicz długości odcinków, na które prosta k podzieliła boki AB i BC

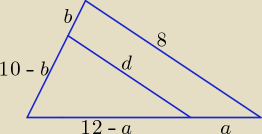
Bogdan: 12 − a + d + 10 − b = a + 8 + b + d ⇒ 14 = 2a + 2b ⇒ 7 = a + b

12		10
	=		⇒ 120 − 12b = 120 − 10a ⇒ 6b − 5a = 0
12 − a		10 − b

Dalej sobie sam poradzisz

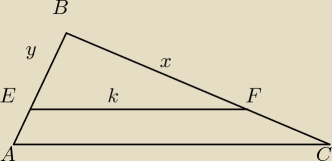
Nienor: Trójkąty ACB i AFB są podobne (kkk). Czyli odpowiednie długości boków są do siebie proporcjonalne.