funkcje ania: wyznacz wszystkie wartości parametru m, dla których równanie: | 3−|x−2| |=m+7 bardzo proszę też o rozpisanie przekształcenia wzoru funkcji po lewej stronie równania

Saizou : l3−lx−2ll−7=m narysuj wykres i odczytaj z wykresu

ania: ale nie wiem co odczytać i jak ten parametr

use: normalnie widzisz że ; m=l3−lx−2ll−7 czyli innymi slowy musisz znalez zbior wrtosci tego wyrazenia l3−lx−2ll−7 bo to jest rowne m

use: czyli m∊<−7;+∞) to widac z rysunku wlasciwie nie trzeba nic liczyc

ania: dziękuję

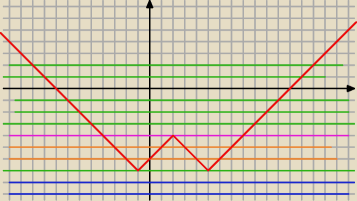
pigor: ..., a więc odczytujesz wartości funkcji g zmiennej m, czyli g(m) liczby punktów przecięcia prostej y=m , m∊R, równoległej do osi Ox (na rys powyżej różnokolorowe) z wykresem funkcji lewej strony y=|3−|x−2||−7 (ta krzywa mocno czerwona) "przesuwając" prostą y=m i piszę sobie wzór funkcji określającej szukane wartości m i tak : { 0 dla m < 7 − nie ma rozwiązań (ma 0 rozwiązań) g(m)= { 2 dla m= −7 lub m > −4 − ma 2 rozwiązania { 3 dla m= −4 − ma 3 rozwiązania { 4 dla −7 < m < −4 − ma 4 rozwiązania , a więc odczytane liczby rozwiązań, to zbiór wartości funkcji g taki {0,2,3,4} dla odpowiednich argumentów m powyżej we wzorze funkcji g . ...

ania: a jeśli do treści zadania dodałabym: "ma więcej rozwiązań dodatnich niż ujemnych" to jak to rozwiązać?

ania: pomożecie?

Mila: Dla m∊(−6,−4)