wartość bezwzględna nierówność Aneczka_93: Witam. mam problem z takim czymś abs(x+2)−x>0 robię to w przedziałach (−∞;−2) , (2;∞) w przedz. (−∞;−2) −x−2−x>0 −2x>2 x<−1 x∊ (−∞;−1) w przedz (2;∞) x+2−x>0 2>0 x∊(−2;∞) Całkowite rozwiązanie to : x∊R

Bogdan: pierwsza część: powinna być odp.: x∊(−∞, −2) druga część powinno być: w przedz. <−2, ∞), odp. x∊<−2, ∞) Odp. końcowa x∊R

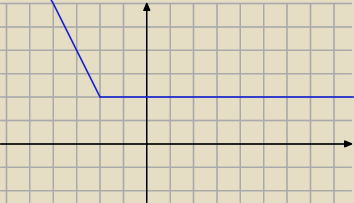
Bogdan: to jest wykres y = |x+2|−x, widać, że y> 0 dla wszystkich x∊R.

Aneczka_93: dzięki Bogdan −całuski ślę , pomyliłam się wpisując −1 w przedziale, ale dobrze myślałam.

Bogdan:

PW: W ramach walki ze schematami myślenia pokażę inne rozwiązanie. |x+2|−x>0 Jest oczywiste, że dla x<0 nierówność jest prawdziwa (lewa strona jest sumą nieujemnej liczby |x+2| i dodatniej liczby −x). Dla x≥0 lewa strona jest równa x+2−x=2, zatem nierówność też jest prawdziwa. Odp. Nierówność jest prawdziwa dla wszystkich x∊R. Nie musieliśmy stosować sakramentalnego "rozbijania na przedziały" dla |x+2|.

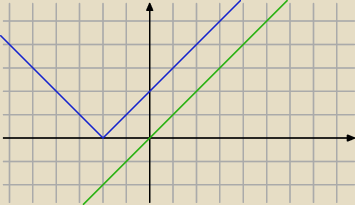
aniabb: albo |x+2|−x>0 to |x−2| > x niebieska > zielona x∊R