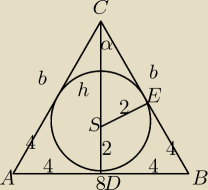
 Podstawa trójkąta równoramiennego ma długość 8,a promień okręgu wpisanego w ten trójkąt jest
równy 2. Oblicz pole tego trójkąta.
Zaczęłam od pola:
P=p*r=1/2(8+2b)*2=8+2b
P=1/2*8*h=4h
4h=8+2b
Potem zaobserwowałam podobieństwo:
ΔSEC∼ΔDBC (kkk)
4/2=b/h−2
I dalej mi nic nie wychodzi, czy popelniłam jakiś błąd? Próbowałam podstawić to co wyliczyłam z
podobieństwa i z pola, ale coś mi to nie wyszło.
Podstawa trójkąta równoramiennego ma długość 8,a promień okręgu wpisanego w ten trójkąt jest
równy 2. Oblicz pole tego trójkąta.
Zaczęłam od pola:
P=p*r=1/2(8+2b)*2=8+2b
P=1/2*8*h=4h
4h=8+2b
Potem zaobserwowałam podobieństwo:
ΔSEC∼ΔDBC (kkk)
4/2=b/h−2
I dalej mi nic nie wychodzi, czy popelniłam jakiś błąd? Próbowałam podstawić to co wyliczyłam z
podobieństwa i z pola, ale coś mi to nie wyszło.
| 2 | 4 | ||
= | |||
| h−2 | b+4 |
| 16 | ||
h= | ||
| 3 |
| 64 | ||
odp: P= | [j2]] | |
| 3 |

