 x2−4x+y2−2y=8
(x−2)2−4+(y−1)2−1=8
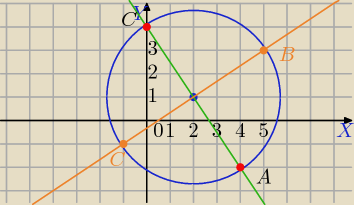
(x−2)2+(y−1)2=13 postać kanoniczna
S=(2,1), r=√13
k: 3x+2y−8=0
x2−4x+y2−2y=8
(x−2)2−4+(y−1)2−1=8
(x−2)2+(y−1)2=13 postać kanoniczna
S=(2,1), r=√13
k: 3x+2y−8=0
| −3 | ||
k: 2y=−3x+8⇔y= | x+4 | |
| 2 |
| −3 | −3 | |||
x2−4x+( | x+4)2−2*( | x+4)=8 | ||
| 2 | 2 |
| 9 | ||
x2−4x+ | x2−12x+16+3x−8=8 | |
| 4 |
| 13 | |
x2−13x=0 | |
| 4 |
| 13 | ||
x( | x−13)=0⇔ | |
| 4 |
| −3 | −3 | |||
y= | *0+4=4 lub y= | *4+4=−2 | ||
| 2 | 2 |
| 2 | 2 | −1 | ||||
BD: y= | x+b i 1= | *2+b⇔b= | ||||
| 3 | 3 | 3 |
| 2 | 1 | |||
y= | x− | równanie prostej zawierającej przekątną BD | ||
| 3 | 3 |
| 2 | 1 | 2 | 1 | |||||
x2−4x+( | x− | )2−2( | x− | )=8 | ||||
| 3 | 3 | 3 | 3 |