 x2+y2+2x+2y=m2−2,
(x2+2x+1)−1+(y2+2y+1)−1=m2−2⇔
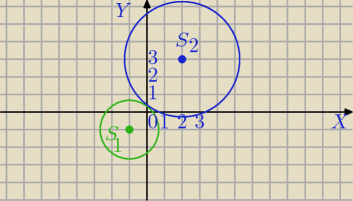
(x+1)2+(y+1)2=m2 postać kanoniczna, S1=(−1,−1),r=m
x2+y2−4x−6y=4m2−13
(x2−4x)+(y2−6y)=4m2−13 Uzupelniam wyrażenia w nawiasach do kwadratów wyrażeń
(x2−4x+4)−4 +(y2−6y+9)−9=4m2−13
(x−2)2+(y−3)2=4m2 , S2=(2,3), R=2m
okręgi są zewnętrznie styczne gdy
|S1S2|=r+R
m+2m=√32+42
3m=5
x2+y2+2x+2y=m2−2,
(x2+2x+1)−1+(y2+2y+1)−1=m2−2⇔
(x+1)2+(y+1)2=m2 postać kanoniczna, S1=(−1,−1),r=m
x2+y2−4x−6y=4m2−13
(x2−4x)+(y2−6y)=4m2−13 Uzupelniam wyrażenia w nawiasach do kwadratów wyrażeń
(x2−4x+4)−4 +(y2−6y+9)−9=4m2−13
(x−2)2+(y−3)2=4m2 , S2=(2,3), R=2m
okręgi są zewnętrznie styczne gdy
|S1S2|=r+R
m+2m=√32+42
3m=5
| 5 | ||
r=m= | ||
| 3 |
| 10 | ||
R= | ||
| 3 |