Geometria Piotruś: W trójkącie prostokątnym przyprostokątne mają długość 12cm i 5cm. Przez wierzchołek kąta prostego poprowadzono prostą, która podzieliła ten trójkąt na dwa trójkąty o równych obwodach. Oblicz stosunek promieni okręgów wpisanych w powstałe trójkąty. Nie wiem jak wyznaczyć długość tej prostej przechodzącej przez kąt prosty. Proszę o pomoc w jej obliczeniu.

Maciek: przeciwprostokątna wyjdzie 13 z Pitagorasa zgadza się?

Maciek: tą prostą która go podzieliła oznacz sobie jako "x"

Maciek: przeciwprostokątną jako "a" i "b" razem dają 13

Maciek: skoro mają równe obwody to możemy zapisać, że 5+x+a=12+x+b

Maciek: "x" się skasują

Maciek: 5+a=12+b oraz a+b=13

Maciek: po wyliczeniu układu równań a=10 b=3

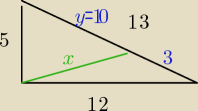
aniabb: tak ta prosta ma długość x taką że 5+x+y=12+x+(13−y) 2y=20 y=10 więc teraz z tw cos x²=12²+3²−12•3•12/13

Piotruś: Tak, to już obliczyłem.

Piotruś: Dzięki

Piotruś: A chciałoby się komuś z Was to obliczyć do końca? Mi wychodzą popaprane liczby, a nie ma odpowiedzi do tego zadania w książce.

aniabb: zjadłam 2 przed ab x²=144+9−2•144•3/13 x≈9,3 co w sumie nie jest potrzebne r=2P/(a+b+c) r₁ /r₂= P₁ / P₂ P₁ = 30−90/13 = 300/13 P₂ = 6•15/13 = 90/13 r₁ /r₂= 300/90 = 10/3

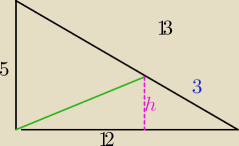
aniabb: h/3=5/13 więc h=15/13