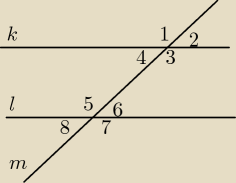
Dwie proste równoległe k i l przecięto prostą m. wajdzik: Dwie proste równoległe k i l przecięto prostą m. Udowodnij, że dwusieczne kątów naprzemianległych są równoległe. Kąty naprzemianległe wewnętrznie 3 i 6 V 4 i 5 Kąty naprzemianległe zewnętrznie 1 i 8 V 2 i 7 Kąty odpowiadające 1 i 5 V 3 i 7 V 2 i 6 V 4 i 8 Jeżeli dwie proste równoległe przetniemy trzecią prostą, to utworzone kąty: −naprzemianległe mają równe miary −odpowiadające mają równe miary Jeżeli dwie proste tworząz trzecią kąty naprzemianległe wewnętrznie równe, to są do siebie równoległe. Co tutaj mogę jeszcze dodać?

wredulus_pospolitus: to co napisałes to jest wstęp do rozwiązania zadania ... ale nigdzie nie ma informacji, że ów dwusieczne są równoległe. najłatwiej po prostu narysować dwusieczną kąta (np. 2) i przedłużyć ją do przecięcia z prosta l ... skorzystać z tego co napisałeś do pokazania że kąt 2' i l6' są równe analogicznie zrobić z dwusieczną kąta 6 teraz wystarczy napisać, że kąt l6' oraz 6' są sobie równe ... więc te dwie dwusieczne są równoległe

wajdzik: Mógłbyś pokazać mi te przecięcia na rysunku? Bo nie wiem czy dobrze myślę.

wajdzik:

Janek191: Te kąty naprzemianległe są źle wypisane ! Kąty naprzemianległe wewnętrzne, to: 4 i 6 , 3 i 5 Kąty naprzemianległe zewnętrzne, to : 1 i 7; 2 i 8

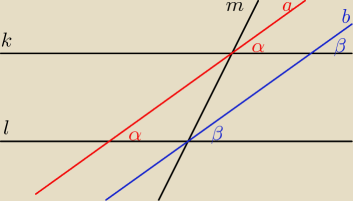
wredulus_pospolitus: niebieska i czerwona linia to te dwie dwusieczne (z ich przedłużeniami) i piszesz: α = 0.5*kąt wyjściowy(nr2) β = 0,5*kąt wyjąciowy(nr6) z jakiegoś tam twierdzenia o kątach (podałeś go) kąt nr2 i nr 6 są równe czyli α=β czyli a || b

Janek191: Zostało udowodnione dla kątów odpowiadających, a nie naprzemianległych

wredulus_pospolitus: Janek −−− tak dla odpowiadających ... ale korzystając z tw. o kątach naprzemiennych przy dwóch prostych przecinających się (kurde ... nie pamiętam nazw) wynika reszta

Janek191: Właśnie w tym jest problem, że "coś " obliczamy, a nie wiemy co to jest to "coś"

PW: @Janek191: Tak jest. Coś dzwoni, ale nie wiadomo, w którym kościele. Kiedyś w rozwiązaniu korzystaliśmy z nierówności trójkąta. Zadałem "głupie pytanie": co to jest? Definicja, pewnik, czy może twierdzenie? Nie było chętnych.

aniabb: ale jak powiesz że z nierówności trójkąta wynika paradoks bliźniąt to może ktoś zajrzy do wikipedii

wajdzik: a ja powiem, że nie rozumiem geometrii i źle się z tym czuję. Aczkolwiek jest ona bardzo ważna więc będę walczyć dopóki mnie nie rozsadzi

wajdzik: Dzięki za pomoc, już zabieram się do pracy.

jkjk: ♥\