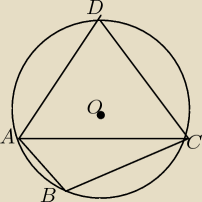
Wierzchołki trójkątów ABC i ACD, o wspólnej podstawie AC, leżą na okręgu. Trójką Ania: Wierzchołki trójkątów ABC i ACD, o wspólnej podstawie AC, leżą na okręgu. Trójkąt ACD jest równoramienny, |AD| = |DC|. W trójkącie ABC mamy dane: BC = 8 oraz AC = AB + 6, kąt ABC = 120 stopni Oblicz obwód czworokąta ABCD. Wiem, że należy użyć twierdzenia sinusów, ale jak?

Bogdan:

	1
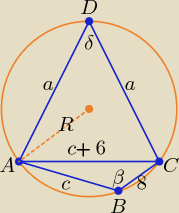
β = 120o, cos120o = cos(180o − 60o) = −cos60o = −
	2

δ = 180^o − 120^o = 60^o (w czworokącie wpisanym w okrąg sumy miar kątów przeciwległych są równe 180^o) Trójkąt ACD jest równoboczny: a = c + 6, Na podstawie twierdzenia cosinisów w trójkącie ABC:

	1
(c + 6)2 = c2 + 64 + 2*8*c*		⇒ c = 7 i a = 7 + 6 = 13
	2

Ania: dziękuję