Funkcja bezendu:

	x2+4x+5
Funkcja f określona jest wzorem f(x)=		. Wykres funkcji f przesunięto o wektor
	x2+4x

u=[p,0] otrzymując wykres funkcji g. Znajdź wzór funkcji g i współrzędne wektora u wiedząc, że wykres funkcji g jest symetryczny względem osi OY jak względem osi OY to f(−x)

	(−x)2+4(−x)+5
f(−x)=		=
	(−x)2+4(−x)

	x2−4x+5
=		ok
	x2−4x

Patronus: No tak, tylko jeszcze przesunięcie o wektor u = [p,0] Czy w efekcie:

	(−x − p)2 + 4(−x−p) + 5
g(−x) =		=
	(−x−p)2 + 4(−x−p)

	(x − p)2 + 4(x−p) + 5
=		= g(x)
	(x−p)2 + 4(x−p)

i teraz trzeba wyliczyć p.

irena_1:

	x2+4x+5		5
f(x)=		=1+
	x2+4x		x2+4x

g(x)=f(x−p)

	5
g(x)=1+
	(x−p)2+4(x−p)

Wykres funkcji g jest symetryczny względem osi OY, czyli g(−x)=g(x)

	5		5
1+		=1+
	(−x−p)2+4(−x−p)		(x−p)2+4(x−p)

(−x−p)²+4(−x−p)=(x−p)²+4(x−p) x²+2px+p²+4x−4p=x²−2px+p²+4x−4p 4px=8x p=2

bezendu: ok

x2−2xp+p2+9
	?
x2−2x+p2

bezendu: O już jest rozwiązanie... Dziękuje

bezendu: a jeszcze wracając do wskazówki Patronusa

(−x−p)2+4(−x−p)+5
(−x−p)2+4(−x−p)

mogę skrócić (−x−p) wtedy miałbym

x2−2xp+p2+9
x2−2xp+p2

Patronus: nie możesz tego skrócić bo masz ssmę − musiałbyś wszystkie czynniki sumy podzielić przez (−x−p),

bezendu:

x2+2xp+p2−4x−4p+5
	i co dalej z tym ?
x2+2xp+p2−4x−4p

bezendu: ?

Patronus: a gdzie masz równanie − znak "=" gdzieś zginął. Jak się pojawi to rozwiązuj równanie za względu na p, iksy powinny sie w końcu skrócić

bezendu: jak mam równianie do zajmuję się tylko licznikiem x²+2xp+p²−4x−4p+5=0

bezendu:

bezendu:

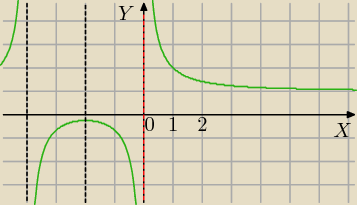
Mila: Aby wykres g(x) miał os symetrii po translacji to f(x) musi mieć oś symetrii. Os symetrii f(x): D: x²+4x≠0⇔ x≠0 i x≠−4 x=−2 oś symetrii f(x) [p,0]=[2,0] Wynik jak u IRENY

asdf: funkcja parzysta

bezendu: ale chodzi mi o wyznaczenie p ze wzoru Petronusa

Mila: Sprawdzam.

	(x−2)2+4(x−2)+5		x2−4x+4+4x−8+5
g(x)=		=
	(x−2)2+4(x−2)		x2−4x+4+4x−8

	x2+1
g(x)=
	x2−4

Czy g(−x)=g(x)

	(−x)2+1		x2+1
g(−x)=		=		=g(x)
	(−x)2−4		x2−4

wektor [2,0] spełnia warunki zadania.

bezendu: Ok dziękuje ślicznie

Mila: Rozpisujemy ułamki:

(−x − p)2 + 4(−x−p)		5
	+		=
(−x−p)2 + 4(−x−p)		(−x−p)2 + 4(−x−p)

(x − p)2 + 4(x−p)		5
	+		⇔
(x−p)2 + 4(x−p)		(x−p)2 + 4(x−p)

	5		5
1+		=1+		⇔
	(−x−p)2 + 4(−x−p)		(x−p)2 + 4(x−p)

5		5
	=		⇔
(−x−p)2 + 4(−x−p)		(x−p)2 + 4(x−p)

Liczniki równe to mainowniki też muszą być równe: (−x−p)² + 4(−x−p)=(x−p)² + 4(x−p)⇔ x²+2px+p²−4x−4p=x²−2px+p²+4x−4p⇔ 2px−4x=−2px+4x 4px−8x=0⇔4x(p−2)=0⇔ x=0 lub p=2