Funkcja bezendu:

	x−1
Wykres funkcji f(x)=		przekształcone w symetrii względem prostej x=−1 i otrzymano
	x+1

wykres funkcji g. Wyznacz wzór funkcji g przesunięcie o wektor u[1,0]

x+1−1		x
	=
x+1+1		x+2

teraz przesunięcie o wektor −u [−1,0]

x−1		x−1		x+1−2		−2
	=		=		=1−
x−1+2		x+1		x+1		x+1

ok ?

asdf: dobrze

asdf: o, a tu masz te 2 wykresy: http://www.wolframalpha.com/input/?i=y+%3D+%28x-1%29%2F%28x%2B1%29+and+y+%3D+1+%2B+2%2F%28x%2B1%29

bezendu: ok dzięki ale chyba jeszcze powinno być względem osi OY ?

asdf: względem osi OY ⇔ względem x = 0

Kostek: asdf chyba nie do końca mi się to podoba najpierw masz o wektor u [1,0]

x−1−1		x−2
	=
x−1+1		x

teraz względem osi OY czyli f(−x)

−x−2		x+2
	=
−x		x

i teraz dopiero o wektor −u[−1,0]

x+1+2		x+3
	=
x+1		x+1

x+1+2		2
	=1+
x+1		x+1

asdf: @Kostek z wyniku wnioskowalem, ze ma dobrze, ale masz racje

Kostek:

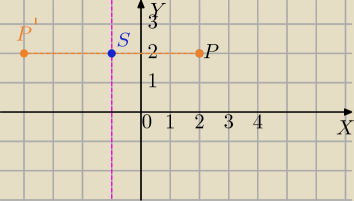
Mila: Niech P '(x',y') będzie obrazem punktu P(x,y) względem prostej x=−1 S=(−1,y) jest środkiem odcinka PP'

	x'+x
−1=		⇔−2=x'+x⇔x'=−2−x oraz x=−2−x'
	2

y'=y

	x−1
f(x)=
	x+1

	−2−x'−1
y'=
	−2−x'+1

	−x'−3
y'=
	−x'−1

	x'+3
y'=		opuszczamy znaczki '
	x'+1

	x+3
g(x)=
	x+1

W nowym wątku narysuję.

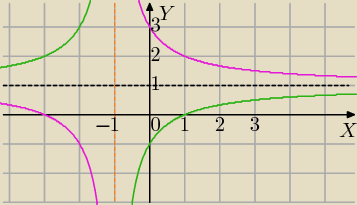
Mila: W poprzednim wątku wyprowadziłam Ci wzór na takie przekształcenie symetria względem prostej x=m x'=2m−x y'=y

	x−1
f(x)=
	x+1

	x+3
g(x)=
	x+1

bezendu: Dziękuje ślicznie a przekształcenie @Kostka jest nie dobre ?

Cusack: dobre, Mila podała inny sposób. tutaj podobnie jak Kostek: http://www.zadania.info/1243707

bezendu: Mila możesz mi wytłumaczyć pierwszą linijkę ?

Mila: Ja podałam ogólny sposób. Sposób Kostka dobry. Nie widziałam, że to zrobił, a zauważyłam błąd w Twoim rozwiązaniu.

Mila: Nie wiem który zapis, najlepiej skopiuj.

bezendu:

	x'+x
−1=		o to chodzi
	2

Mila: S=(−1,y) to środek odcinka PP' P=(x,y) , P'=(x',y')

	x'+x
xs=
	2

	y'+y
ys=		wzory na współrzędne środka odcinka
	2

za x_s podstawiłam −1

Mila: Dobranoc

bezendu: Dobranoc i jeszcze raz dziękuje