Trapez równoramienny opisany na okręgu. Paweł: Pole trapezu równoramiennego opisanego na okręgu jest równe 72√3. Oblicz długości podstaw tego trapezu, wiedząc, że jego ramię jest nachylone do podstawy pod kątem 60*.

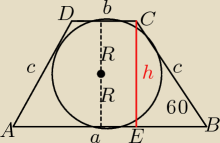
Mila: a+b=2c, h=2R

	1
P=		*2c*h⇔72√3=c*h
	2

	1
W Δ CEB: EB=		c
	2

	c√3
h=
	2

	c√3
72√3=c*h⇔72√3=c*		⇔
	2

144=c² c=12 EB=6 a+b=2c 2b+2*EB=2*12 2b+2*6=24 2b=12 b=6 a=b+2*6=18 odp. a=18 b=6

Paweł: Nie rozumiem trzeciej linijki, mogłabyś jakoś dokładniej wyjaśnić?

Mila: W ΔCEB kąty mają miary: 60,30,90 czyli połowa Δ równobocznego o boku c. (CE jest osią symetrii Δ równobocznego o boku c)

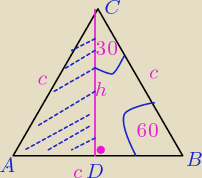
Mila: ΔCDB jest połową ΔABC

	1
DB=		c
	2

Klara:

Klara: