Przeprowadzenie prostego dowodu dotyczącego środkowej w trójkącie prostokątnym dziabaducha12: Udowodnij, że jeżeli środkowa trójkąta równa się połowie boku, do którego została poprowadzona, to trójkąt jest prostokątny

Artur_z_miasta_Neptuna: środkowa dzieli kąt (z którego jest poprowadzona) na połowę to należy wyciągnąć odpowiednie wnioski:

	środkowa		środkowa
ctgα =		=
	lewa strona podstawy		prawa strona podstawy

stąd wniosek −> środkowa dzieli podstawę na pół oraz jej długość = 0,5*podstawa (na którą pada) ... tgα = 1 −> α = 45^o czyli kąt który podzieliła ów środkowa jest kątem prostym. c.n.w.

Klara:

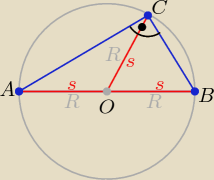
irena_1: Można też tak: O− środek boku AB trójkąta ABC. |OA|=|OB|=|OC|, czyli punkt O jest równo odległy od wszystkich wierzchołków trójkąta ABC. Punkt O jest więc środkiem okręgu opisanego na trójkącie ABC. Ponieważ punkt O to środek boku AB, więc kąt ABC− kąt wpisany w okrąg− jest oparty na średnicy okręgu. Jest więc kątem prostym. Wniosek− trójkąt ABC jest trójkątem prostokątnym.