oblicz kąty utworzone przez dwusieczne kątów zewnętrznych i wewnętrznych Gabriela: W trójkącie ABC dane są kąty wewnętrzne A = 30^o i B=40^o . Oblicz miarę kąta: a) między dwusiecznymi kątów zewnętrznych, utworzonych przy wierzchołkach A i B. b) między dwusieczną kąta wenętrznego A i dwusieczną kąta zewnętrznego przy wierzchołku B. c) między prostymi zawierającymi wysokości opuszczone z wierzchołka A i z wierzchołka B. d) między prostą zawierającą wysokość poprowadzoną z wierzchołka B i dwusieczną kąta zewnętrznego przy wierzchołku A. Próbowałam to jakoś rozwiązać ale zawsze wychodzi mi to jakoś inaczej, w internecie są odpowiedzi ale zależy mi na zrozumieniu tego zadania więc prosiłabym przede wszystkim o rysunki bo jakoś nie potrafię sobie tego wyobrazić dlaczego wychodzi tak, a nie inaczej. Z góry dziękuję za pomoc !

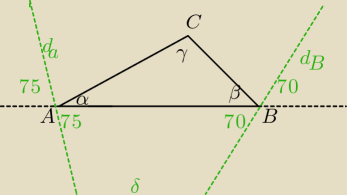
Mila: α=40 β=30 γ=110 a)180−30=150; 150:2=75 180−40=140; 140:2=70 δ=180−(75+70)=180−145=35 nie zmieścił się cały rysunek, masz przedłużyć w dół dwusieczną d_a i d_B dalej chyba poradzisz sobie?