 Dana jest funkcja f(x)=(x−2)(|x|−2). Naszkicuj wykres tej funkcji. Na jego podstawie podaj
liczbę rozwiązań równania f(x)=m+1 w zależności od parametru m.
Wyszły mi takie warunki
f(x)=(x−2)2 dla x≥o
f(x)=−(x−2)2 dla x<0
Na zielono zaznaczyłam to co mi wyszło i teraz jak z tym parametrem, gdyby nie do 1, to bym
wiedziała, i ogólnie czy to dobrze robie?
Dana jest funkcja f(x)=(x−2)(|x|−2). Naszkicuj wykres tej funkcji. Na jego podstawie podaj
liczbę rozwiązań równania f(x)=m+1 w zależności od parametru m.
Wyszły mi takie warunki
f(x)=(x−2)2 dla x≥o
f(x)=−(x−2)2 dla x<0
Na zielono zaznaczyłam to co mi wyszło i teraz jak z tym parametrem, gdyby nie do 1, to bym
wiedziała, i ogólnie czy to dobrze robie?
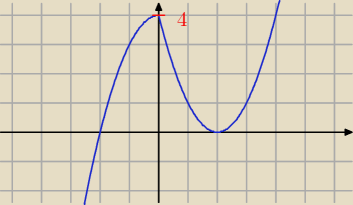 y = (x − 2)(|x| − 2)
Dla m + 1 < 0 ⇒ m < −1 jedno rozwiązanie
dla m + 1 = 0 ⇒ m = −1 dwa rozwiązania
dla 0 < m + 1 < 4 ⇒ −1 < m < 3 trzy rozwiązania
dla m + 1 = 4 ⇒ m = 3 dwa rozwiązania
dla m + 1 > 4 ⇒ m > 3 jedno rozwiązanie.
y = (x − 2)(|x| − 2)
Dla m + 1 < 0 ⇒ m < −1 jedno rozwiązanie
dla m + 1 = 0 ⇒ m = −1 dwa rozwiązania
dla 0 < m + 1 < 4 ⇒ −1 < m < 3 trzy rozwiązania
dla m + 1 = 4 ⇒ m = 3 dwa rozwiązania
dla m + 1 > 4 ⇒ m > 3 jedno rozwiązanie.