Jutro mam z tego spr. Pomocy Natalia: 1.Na boku BC trójkąta równobocznego ABC wybrano punkt M taki, że BM=1/3MC. Wykaż ,że sinus kąta CAM jest równy (3√39)/26. 2.W trójkącie ABC mamy dane |AC|=4, |BC|=|AB|−2 oraz kąt ACB=60^. Oblicz sinusy kątów CAB i ABC.

Natalia: Da ktoś radę rozwiązać.

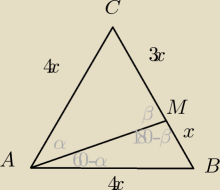
Saizou : w ΔACM

3x		4x
	=
sinα		sinβ

4x*sinα=3x*sinβ 4sinα=3sinβ w ΔABM

4x		x
	=
sin(180−β)		sin(60−α)

4x*sin(60−α)=x*sin(180−β) 4sin(60−α)=sin(180−β) 4sin(60−α)=sinβ 4sinα=3*4sin(60−α)

	√3		1
sinα=3sin(60−α) sin(60−α)=sin60cosα−cos60sinα=		cosα−		sinα
	2		2

	√3		1
sinα=3(		cosα−		sinα) /*2
	2		2

2sinα=3√3cosα−3sinα 5sinα=3√3cosα

	5
cosα=		sinα
	3√3

korzystając z jedynki trygonometrycznej

	25
sin2α+		sin2α=1
	27

27sin²α+25sin²α=27 52sin²α=27

	27
sin2α=
	52

	3√39
sinα=		, bo α∊ I ćwl
	26

Bogdan:

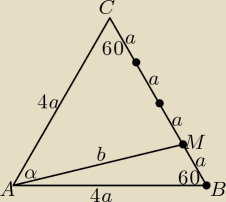
	1		1
sin60o =		cos60o =
	2		2

W trójkącie ABM z twierdzenia cosinusów:

	1
b2 = 16a2 + a2 − 2*4a*a*		= 13a2 ⇒ b = a√13
	2

W trójkącie AMC z twierdzenia sinusów:

3a		b
	=		stąd wyznacz sinα
sinα		sin60o

Saizou :

	√3
Bogdanie masz chochlika sin60o=
	2

Bogdan:

	√3
Tak, dziękuję sin60o =
	2

Bogdan:

	√3   3a *   2
sinα =		= ...
	a√13

Saizou : a ja się tak namęczyłem