W ostrosłupie ABCS podstawa ABC Maniek: W ostrosłupie ABCS podstawa ABC jest trójkątem równobocznym o boku długości a. Krawędź AS jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka A od ściany BCS jest równa d. Wyznacz objętość tego ostrosłupa.

Dziabong: http://www.edulandia.pl/matura/1,118553,13883056,Matura_2013__matematyka__poziom_rozszerzony___odpowiedzi.html?as=2

Janek191: Dane : a , d a = I AB I = I BC I = I AC I h₁ = I AD I − wysokość podstawy ostrosłupa

	√3		3
h1 = a		⇒ h12 =		a2
	2		4

h = I AS I − wysokość ostrosłupa h₂ = I DS I = x + y − wysokość Δ BCS d = I AE I − odległość A od ściany BCS Niech x = I SE I , y = I DE I Trójkąt prostokątny AES jest podobny do trójkąta prostokątnego DAS ( mają takie same kąty ) Mamy więc

d		h1
	=		⇒ h*h1 = d*( x + y)
h		x + y

oraz ( x + y)² = h² + h₁² ⇒ x + y = √ h² + h₁² zatem h*h₁ = d* √ h² + h₁² / : d

h*h1
	= √ h2 + h12 ; podnoszę obustronnie do kwadratu
d

h2*h12
	= h2 + h12
d2

	h12
(		− 1)* h2 = h12
	d2

	3
Wstawiam		a2 za h12
	4

	3 a2		3
(		− 1)* h2 =		a2
	4 d2		4

	3 a2 − 4 d2		3 a2
(		)*h2 =
	4 d2		4

	3 a2		4 d2		3 a2 d2
h2 =		*		=
	4		3 a2 − 4 d2		3 a2 − 4 d2

więc

	a d √3
h =
	√ 3 a2 − 4 d2

================= P_p − pole podstawy ostrosłupa

	a2 √3
Pp =
	4

=========== Objętość ostrosłupa

	1		1		a2 √3		a d √3
V =		Pp *h =		*		*
	3		3		4		√ 3 a2 − 4 d2

	a3 d
V =
	4 √ 3 a2 − 4 d2

======================

	3
d < h1 ⇒ d2 < h12 =		a2
	4

więc

	3
4 d2 < 4*		a2 = 3 a2 ⇒ 3 a2 − 4 d2 > 0
	4

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

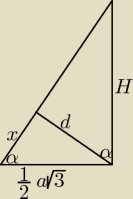Bogdan: Mozna prościej, np. tak:

	1		x		d
x = √ 3a2/4 − d2 =		√3a2 − 4d2,		=
	2		1   a√3 2		H

	1   a√3 * d 2		1   a√3 * d 2
H =		=
	x		1   √3a2 − 4d2 2

	1		1		a√3 * d		a3d
V =		*		a2√3 *		=
	3		4		√3a2 − 4d2		4√3a2 − 4d2

łukasz 195: Czy objętość mogła wyjść v=a³/8?.

Janek191: Nie mogła wyjść taka objętość.