Prosta o równaniu x przecina okrąg o środku S Gob: Prosta o równaniu 3x−4y−36=0 przecina okrąg o środku S=(3,12) w punktach A i B. Długość odcinka AB jest równa 40. Wyznacz równanie tego okręgu.

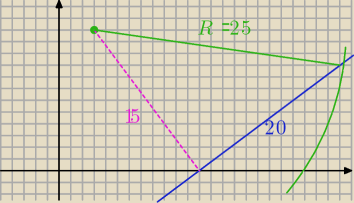
Kaja: 1.wyznacz równanie prostej prostopadłej do danej prostej 2. wyznacz punkt przecięcia danej prostej i wyznaczonej prostej prostopadłej (punkt D) 3. wyznacz długość odcinka SD 4. z Tw. Pitagorasa wyznacz długość odcinka AS (to będzie promień tego okręgu) − tu rozważ sobie trójkąt prostokątny ASD 5. zapisz równanie okręgu

camus: 1)znajdź odległość między prostą a środkiem okręgu 2)zauważ, że połowa cięciwy (ten kawałek prostej, która "jest" w okęgu) i odległość między prostą a środkiem okręgu to przyprostokątne trójkąt prostokątnego, a promień to przeciwprostokątna tego trójkąta (zrób sobie rysunek) 3)polub twierdzenie pitagorasa

aniabb: (x−3)²+(y−12)²=625

xyz: zadanie na 3 min roboty a dawali 5 pkt ^^

aniabb: