 CHodzi mi, żeby WYPROWADZIĆ !
CHodzi mi, żeby WYPROWADZIĆ !
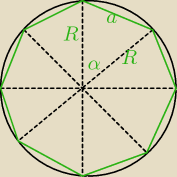 a− długość boku ośmiokąta foremnego
α=360:8=450
z tw cosinusów
a2=R2+R2−2*R2*cos450
a− długość boku ośmiokąta foremnego
α=360:8=450
z tw cosinusów
a2=R2+R2−2*R2*cos450
| √2 | ||
a2=2R2−2R2* | ||
| 2 |
| a2 | ||
R2= | ||
| 2−√2 |
| a | ||
R= | ||
| √2−√2 |

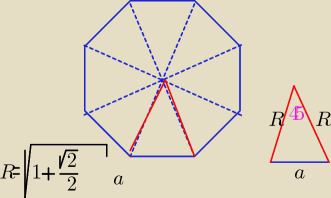 360o: 8= 45o
trójkąt równoramienny o ramionach R, R podstawie a i kącie między ramionami 45o
z twierdzenia kosinusów
a2=R2+R2−2R*R*cos45o
360o: 8= 45o
trójkąt równoramienny o ramionach R, R podstawie a i kącie między ramionami 45o
z twierdzenia kosinusów
a2=R2+R2−2R*R*cos45o
| √2 | ||
2R2−2R2 | = a2 | |
| 2 |
| √2 | ||
R= √1+ | *a | |
| 2 |



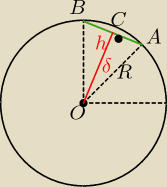 Jeśli bez tw. cosinusów to tak:
W ΔAC):
Jeśli bez tw. cosinusów to tak:
W ΔAC):
| ||||||||
sinδ= | ||||||||
| R |
| ||||||||
sin22,50= | ||||||||
| R |
| √2 | ||
cos450= | ||
| 2 |
| 1 | 1 | |||
sin2(22,5)= | − | cos45 | ||
| 2 | 2 |
| 1 | 1 | √2 | 2−√2 | |||||
sin2(22,5)= | − | * | = | |||||
| 2 | 2 | 2 | 4 |
| √2−√2 | ||
sin(22,5)= | ||
| 2 |
| a | ||
R= | dokoncz | |
| 2sin(22,5) |