.. mat: Czy mógłby mi ktoś wytłumaczyć krok po kroku jak robić zadanie tego typu ? A, B są zdarzeniami losowymi zawartymi w Ω. Wykaż, że jeżeli P(A) = 0,9 i P(B)= 0,7 to P(A∩B') ≤ 0,3 (B'oznacza zdarzenie przeciwne do zdarzenia B)

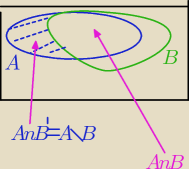
Mila: A∩B'=A\B P(A∪B)=P(A)+P(B)−P(A∩B)=0,9+0,7−P(A∩B)≤1 ( z własności prawd.) 1,6−P(A∩B)≤1⇔0,6≤P(A∩B) P(A∩B')=P(A)−P(A∩B)=0,9−P(A∩B)≤0,9−0,6=0,3 ⇔ (odjęliśmy mniej lub tyle samo, co P(A∩B), zatem różnica ≤0,3) P(A∩B')≤0,3

Mila: Dodaję wyjaśnienie: P(A\B)=P(A)−P(A∩B)

mat: ok, dziękuje jak będę miał jakieś wątpliwości to zapytam jeszcze

Mila:

mat: Mam pytanko odnośnie do tego: P(A\B)=P(A)−P(A∩B) z czego jest to wyprowadzone ?

blendi: z rysunku jak masz P(A\B) to jest to zakreskowane a jest to równe P(A)−P(A∩B) czyli jak od całego zbioru A odejmiesz część wspólną A i B

Mila: Liczysz jak pole.

mat: Ok, dziękuje Wam bardzo