Wykaż, że i wyznacz stosunek media: Dany jest trójkąt równoboczny ABC. Punkty P, Q, R leżą na bokach trójkąta ABC (po jednym punkcie na każdym boku) w taki sposób, że każdy bok trójkąta PQR jest prostopadły do jednego boku trójkąta ABC. a) wykaż, że trójkąt PQR jest równoboczny. b) Wyznacz stosunek ^|AB|_|PQ| Bardzo bym prosiła o pomoc tylko bez stosowania sinusów, itp bo tego jeszcze nie mieliśmy.

media: Pomoże ktoś może ?

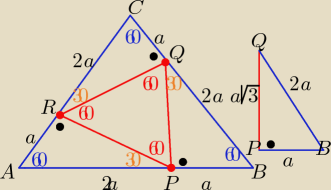
Eta: 1 sposób Trójkąty APR, BPQ, CRQ są prostokątne o kątach 30^o,60^o, 90^o zatem kąty P , R, Q mają miary: 180^o−(30^o+90^o)= 60^o czyli trójkąt PQR jest równoboczny 2 sposób z trójkąta prostokątnego o kątach 30,60,90 długości boków trójkąta PQR są równe |PQ|=|PR|=|RQ|= a√3 zatem trójkąt PQR jest równoboczny

	|AB|		3a		3
b)		=		=		= √3
	|PQ|		a√3		√3

media: a skąd wiadomo że będzie a i 2a ?

media: ahh juz wiem dziękuje za rozwiązanie

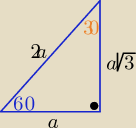
Eta: Z własności trójkąta o kątach 30^o,60^o ,90^o

Eta:

PW: Weź trójkąt PBQ (bez napisów określających długości boków, jedynie z miarami kątów) i dostaw do niego symetryczny wzgledem PQ − zobaczysz trójkąt równoboczny B'BQ, a w nim − wiadomo − wysokość QB dzieli podstawę na pół.

Eta: