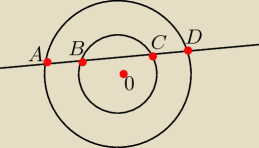
Wykaż że media: Prosta przecina dwa okręgi współśrodkowe odpowiednio w punktach A, D i B, C ja na rysunku. Wykaż, że |AB|=|CD| PILNIE PROSZE O POMOC

Janek191: Prowadzimy prostą EO prostopadłą do pr AD. E ∊ pr AD Niech r − promień mniejszego okręgu ( r = I O B I ) R − promień większego okręgu ( R = I OA I ) I BE i = x i I CE i = y ; I EO I = z Mamy x² = r² − z² oraz y² = r² − z² czyli x² = y² ⇒ x = y −−−−−−−−−−−−−−−−−−−−−−− I AE I² = R² − z² oraz I DE I² = R² − z² więc I AE I = I DE I dlatego I AB I = I AE I − x oraz I CD I = I DE I − x , ale I AE I = I DE I więc I AB I = I CD I ckd.

Janek191: Prowadzimy prostą EO prostopadłą do pr AD. E ∊ pr AD Niech r − promień mniejszego okręgu ( r = I O B I ) R − promień większego okręgu ( R = I OA I ) I BE i = x i I CE i = y ; I EO I = z Mamy x² = r² − z² oraz y² = r² − z² czyli x² = y² ⇒ x = y −−−−−−−−−−−−−−−−−−−−−−− I AE I² = R² − z² oraz I DE I² = R² − z² więc I AE I = I DE I dlatego I AB I = I AE I − x oraz I CD I = I DE I − x , ale I AE I = I DE I więc I AB I = I CD I ckd.

irena_1: Trójkąty BOC i AOD to trójkąty równoramienne. Ich podstawy leżą na tej samej prostej, a ramiona maja wspólny punkt O. Takie trójkąty maja wspólną oś symetrii − to prosta prostopadła do prostej AD, przechodząca przez punkt O. Odcinki AB i CD są odcinkami symetrycznymi do siebie względem tej osi symetrii. Mają więc równą długość.

media: Dziękuje