liczymy deltę i..
Adrian: Dla jakich wartości parametru m miejsca zerowe funkcji f (x) = x2 − (m − 2)x − 2m + 4
należą do przedziału (−1; 1)?
Mam problem z tym zadaniem bo tak. Obliczyłem sobie deltę, wynikiem tego były: m=−6 lub m=2.
Wiem jednak, że te m−y dadzą mi wszystkie rozwiązania, a ja potrzebuję tylko x z zakresu (−1;
1). Jak dalej przycisnąć zadanie?
9 maj 00:42
Akas: Proponuję rozwiązać to graficznie.
9 maj 00:44
Adrian: Mianowicie? Nie za bardzo rozumiem co mam zrobić. W głowie mam dwa wykresy, ale nie wiem czy o
to chodzi bo jak dla mnie nic z nich nie wynika (no może poza tym, że y−greki muszą być
ujemne, aby x mieściły się w przedziale.
9 maj 00:46
Damian: f(x)= x2 − (m − 2)x − 2m + 4
f(x)=2x−(4mx)+4
f(x)=(−2)
f(x)=2
9 maj 00:50
Adrian: Chyba nie za bardzo rozumiem co tu zaistniało..
9 maj 00:53
Eta:
1/ Δ≥0
2/ f(−1)>0
3/ f(1)>0
4/ −1≤xw≤1
9 maj 00:55
Eta:
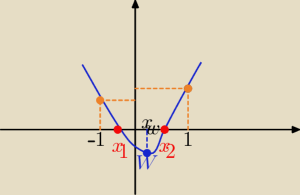
9 maj 00:59
Adrian: Z tego co zasugerowała Eta:
1. m∊(−∞; −6) u (2; ∞)
2. i 3. m<−3
4. 0≤m≤4
Z pierwszego zakresu wynikają wszystkie m, które umożliwiają rozwiązanie.
Z 2 i 3 opcji, rozumiem, że wynika fakt jakie m−y mieszczą się pomiędzy −1 i 1 dla x.
A z opcji numer 4 nie wiem co wynika.
9 maj 01:06
Adrian: Po obejrzeniu obrazka, mam już kompletny mętlik w głowie.
9 maj 01:07
Eta:
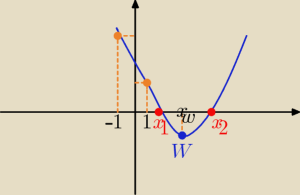
Widzisz co by było gdyby tylko f(−1)>0 i f(1)>0
miejsca zerowe byłyby poza przedziałem (−1,1)
dlatego jeszcze musi być warunek −1<x
w <1
9 maj 01:16
Eta:
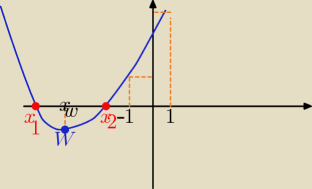
9 maj 01:20
Adrian: Ok. Chyba rozumiem. Rozumiem, że nie ma takich m?
W końcu z tych trzech założeń:
m∊(−∞; −6) u (2; ∞)
m<−3
0≤m≤4
nie mogę uzyskać żadnej wartości.
9 maj 01:21
Eta:
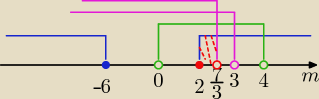
Δ≥0 ⇒ m€(−
∞,−6> U <2,
∞)
| | 7 | |
f(1) >0 ⇒ 1−m+2−2m+4>0 ⇒ m < |
| |
| | 3 | |
f(−1)>0 ⇒ 1+m−2−2m+4>0 ⇒ m<3
x
w> −1 i x
w<1
m−2>−2 i m−2<2 ⇒ m€(0,4)
sprawdź , czy się nie pomyliłam, bo już ledwie na oczy widzę
9 maj 01:43
Adrian: Jest dobrze. Dzięki!

Ja się walnąłem w f(−1). Wyszła mi ujemna 3 przez co za nic w świecie nie mogło być
rozwiązania. Dziękuję raz jeszcze

9 maj 01:49
Eta:

9 maj 01:50

 Widzisz co by było gdyby tylko f(−1)>0 i f(1)>0
miejsca zerowe byłyby poza przedziałem (−1,1)
dlatego jeszcze musi być warunek −1<xw <1
Widzisz co by było gdyby tylko f(−1)>0 i f(1)>0
miejsca zerowe byłyby poza przedziałem (−1,1)
dlatego jeszcze musi być warunek −1<xw <1

 Δ≥0 ⇒ m€(−∞,−6> U <2,∞)
Δ≥0 ⇒ m€(−∞,−6> U <2,∞)
 Ja się walnąłem w f(−1). Wyszła mi ujemna 3 przez co za nic w świecie nie mogło być
rozwiązania. Dziękuję raz jeszcze
Ja się walnąłem w f(−1). Wyszła mi ujemna 3 przez co za nic w świecie nie mogło być
rozwiązania. Dziękuję raz jeszcze 
