TRYGONOMETRIA Kangurek: W trójkącie prostokątnym ABC , kąt przy wierzchołku A jest prosty, zaś |ACB|=60. dwusieczna kąta ACB przecina bok AB w punkcie D, Wykaż, że CB² − 2* DB² = AD² + AC²

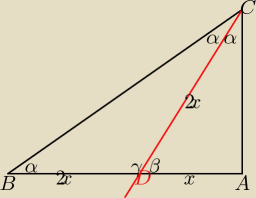
Basia: α=30 β=60 γ=120 BD = DC = 2x AB = ¹₂CD = x CB² = (2x)²+(2x)² − 2*2x*2x*cosγ = 4x²+4x²−8x²*cos120 = 8x²+8x²*¹₂ = 12x² CB² − 2DB² = 12x² − 2*(2x)² = 4x² AD²+AC² = BC² = (2x)² = 4x²

Kangurek: skąd wiemy, że bd = 2x?jakieś twierdzenie?

Krzysiek : https://matematykaszkolna.pl/strona/498.html

Basia: albo trójkąt prostokątny z kątami 30 i 60 (gimnazjum) albo

	AD
sinα =
	CD

	AD
sin30 =
	CD

1		AD
	=
2		CD

CD = 2AD AD = x CD = 2x a trójkąt BDC jest równoramienny bo kąt CBD = kątBDC = 30