Przekątna trapezu równoramiennego ABCD mq: Przekątna trapezu równoramiennego ABCD tworzy z dłuższą podstawą AB kąt α, a z ramieniem AD − kąt β. Wyznacz stosunek pola trójkąta ACD do pola trójkąta ABC.

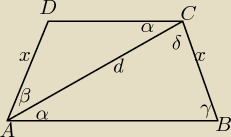
Basia: γ=α+β δ= 180 − α − γ = 180−2α−β = 180 − (2α+β)

	1		1
PABC =		*x*d*sin[180−(2α+β)] =		*x*d*sin(2α+β)
	2		2

	1
PACD =		*x*d*sinβ
	2

PACD		sinβ
	=
PABC		sin(2α+β)

Eta:

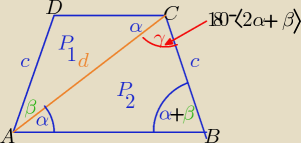
	c*d*sinα		c*d*sinγ		c*d*sin(2α+β)
P1=		, P2=		=
	2		2		2

P1		sinα
	=
P2		sin(2α+β)

Eta:

Eta: No tak .....pomieszało mi nazwy kątów zamiast sinα ma być sin β jak widać na rysunku

mq: mam pytanie. w odpowiedzi jest tg(α+β)−tgα / tg(α+β)+tgα jak do tego dojść?

mq: ?