Matura 2013 prosze o pomoc roch : Dla jakich wartości parametru m równanie sin2x+sinx+m=0 a)ma rozwiązanie b)nie ma rozwiązania 2.Uzasadnij, że liczba log 23 jest niewymierna. I na koniec mam jeszcze takie pytanie jak sie rysuje tego typu funkcje ,np. y=sin³−sin albo y=log²−3log2 +1

wredulus_pospolitus: 1) musisz zauważyć .. że sin2x+sinx ∊ <−2;2> dlaczego najłatwiej z rysunku (narysuj sinx oraz sin2x na tym samym rysunku) stąd a) m∊<−2,2> b) m∊(−∞,−2) u (2,+∞) 2) log 23 co to jest sin³ nie ma czegoś takiego tak samo jak sin albo log² <−−− coś takiego nie istnieje

roch : sorry w pierwszym ma być sin²(x)+sinx+m=0 2 Uzasadnij że liczba logprzypods2 z 3 jest niewymierna

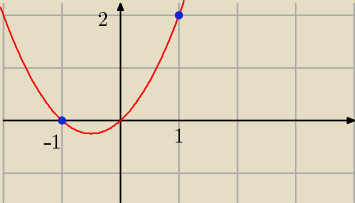
Nienor: sinx=t, t∊[−1,1] t²+t=−m

	−1
Interesujący jest wykres pomiędzy niebieskimi kropkami. Wyliczając q=		można odczytać,
	4

że:

	1
−m≥−		i −m≤2
	4

Grzesiek: wredulus pospolitus a skąd wiadomo że sin(2x) + sin(x) ∊ [−2 ; 2]?

Nienor: T: log₂3∉ℚ D: log₂1<log₂3 0<log₂3 Zakładam, że log₂3 należy do wymiernych, czyli istnieją takie p,q∊ℕ, że:

	p
log23=
	q

log₂3=log₂2^p_q 3=2^p_q 3=2^p*2^−q 3*2^q=2^p A to by oznaczało, że w rozkładzie 2^p występuje 3, a to jest nie możliwe, więc 3*2^q≠2^p, czyli log₂3 jest liczbą niewymierną.

Nienor: Grzesiek sinx maksymalnie może być 1, sin2x też maksymalnie może być 1, a co otrzymasz po dodawniu dwóch jedynek

xyz: Ale −2 to ta funkcja nie osiagnie

Nienor: sinx może minimalnie być −1, tak samo sin2x. Podstawiam: −1+(−1)=−1−1=−2

xyz: Ale tam jest sin²x

Romek: Nienor no coo ty gadasz sin2x maxymalnie może byc 2 a sinx maksymalnie może byc jeden

Romek: xyz wiemy ale ktoś sie potem zapytał dlaczego sin2x +sinx...... ma taki przedział

roch : Niezor to jak bd z tym wykresem ?

roch : A jeśli nie chce robić tego graficznie ? (zad1)

Nienor: Romek powiedz, a dla jakiegoż to x sin2x = 2 roch rozwiązania dotyczą tych poprawionych równań. Musiałabym się zastanowić jak to zrobić nie graficznie i nie zgubić rozwiązań. Ale co jest złego w rozwiązaniu graficznym xyz to odpowiedź na pytanie skąd Artur wiedział, że sin2x+sinx∊[−2,2]

roch : to Panie NIezor Zrób mi Pan to jeszcze raz i wytłumacz na spokojnie dlaczego tak

Nienor: Pani, jak już. Więc przenoszę m na drugą stroną i uzyskuje równanie: sin²x+sinx=−m Sinusy są ogólnie niesympatyczne, więc się ich pozbywam zastępując je t, czyli t=sinx, t∊[−1;1], bo tylko wtedy to podstawienie ma sens. Uzyskuję równanie: t²+t=−m Jeżeli t²+t potraktuję jako funkcję g(t)=t²+t, której dziedziną jest Dg(t)=[−1,1], i −m potraktuję jako funkcję stałą, to rzwiązaniem równania są wszystkie y fukcji g(t), jeżeli t∊[−1,1]. Tak na szczerze, to ciężko to wytłumaczyć na forum, mi przynajmniej.

ZKS: Nienor a dla jakiego argumentu otrzymasz niby że sin(2x) + sin(x) = 2?

Nienor:

	−3		3
Racja, nie dopatrzenie. sin2x+sinx ∊[		;		].
	2		2

ZKS: A skąd ten wynik przecież to czyste strzały i również bo zbiór wartości będzie coś koło ZW = [−1.76 ; 1.76].

roch : Przepraszam Pani Niezor. No dobra i właśnie do tej pory co wytłumaczyłaś rozumiem tylko nie wiem jak to ograniczyć toą funkcję kwadratową

Nienor: Ze zrobionego mniej więcej wykresu. Już liczę pochodną i sprawdzę jak to idzie. Jednak, zgodzę się, że niepoprawnie, taką szkolną metodą, szacuje się w liceach zbiory wartości.

Nienor: Hmm Liczysz p wierzchołka(odczytałam z wykresu) i sprawdzasz, czy p∊[−1;1], jeśli tak to liczysz q wierzchołka, g(−1) i g(1), zbiór wartości funkcji jest rozpięty między wartością najmnieją i największą z wyliczonych. Jeżeli p nie należy do przedziału, to wybierasz wartości z g(−1) i g(1).

ZKS: To sposób algebraiczny przedstawię. sin²(x) + sin(x) + m = 0 sin(x) = t ∊ [−1 ; 1] t² + t + m = 0 1^o Δ ≥ 0 ∧ [f(1) > 0 ∨ f(−1) > 0] Δ = 1 − 4m

	1
1 − 4m ≥ 0 ⇒ m ≤
	4

f(1) ≥ 0 ⇒ 1 + 1 + m ≥ 0 ⇒ m ≥ −2 f(−1) ≥ 0 ⇒ 1 − 1 + m ≥ 0 ⇒ m ≥ 0

	1		1
m ≤		∧ (m ≥ − 2 ∨ m ≥ 0) ⇒ m ∊ [−2 ;		]
	4		4

	1
Dla parametru m ∊ [−2 ;		] mamy rozwiązanie.
	4

ZKS: Oczywiście zwroty powinny być f(1) ≥ 0 ∨ f(−1) ≥ 0.

Ajtek: Cześć ZKS > Gdzie Ty się podziewałeś tyle czasu

ZKS: Witam Ajtek. Ukrywałem się na forum pod innym nickiem. Co tam słychać u Ciebie zdrówko dopisuje?

Ajtek: A dziękuję, zdrówko jest jak było. A dlaczemu się ukrywałeś

pigor: ... , o kurcze, a dlaczego tu f(1) ≥ 0 ∨ f(−1) ≥ 0 masz ∨ zamiast ∧ , przecież t∊ [−1,1]

ZKS: Jak zdrówko dobrze to się cieszę. Jakiś Twój uczeń pisał dzisiaj maturę? A wiesz sam nie wiem tak jakoś wyszło jak przeglądarkę mi jedną walnęło i użyłem innej to wpisałem inny nick i tak pisałem na nim spory okres czasu. Eta wie zapewne który to byłem "ja".

ZKS: Ponieważ dla f(1) ≥ 0 będzie rozwiązanie lub f(−1) ≥ 0 będzie rozwiązanie rozumiesz pigor?

ZKS: Jak nie to zaraz zrobię rysunek o co chodzi.

ZKS: No chyba że coś mi się pomyliło.

Ajtek: Tak pisał, odezwał się do mnie jakieś połgodziny po maturze. Zdać zdał, wynik poznamy w czerwcu . Odnośnie nika to mam typ

Ajtek: A póki co znikam na randkę matematyczną.

ZKS: To pogratulować talentu dydaktycznego. Jak chcesz mogę sprawdzić czy dobrze kombinujesz.

ZKS: Życzę udanej randki.

pigor: ...., moje ∧ wynikło stąd, bo widziałbym całą parabolę zmiennej t=sinx, daną wzorem y=f(t)=t²+t+m i a=1 >0 mającą miejsca zerowe w przedziale [−1;1], czyli jednocześnie na końcach f(−1) ≥ 0 i f(1) ≥0 . −−−−−−−−−−−−−−−−−−−−−− a więc proszę narysuj mi jak to widzisz, bo może mój mózg, nie pracuje już jak należy, bo wcześniej też walnąłem gafę w innym poście i powinienem sobie dać spokój .

ZKS: Zauważ że jeżeli f(−1) ≥ 0 to na pewno będziemy mieli jakieś rozwiązanie nawet jeżeli dla tego m nie będzie spełniona nierówność f(1) ≥ 0 ponieważ nie musimy mięć 2 rozwiązań naraz tylko zadowoli nas już 1 pierwiastek więc f(−1) ≥ 0 ∨ f(1) ≥ 0. Jeżeli f(−1) ≥ 0 dla jakiegoś m ∊ R a dostaniemy że f(1) < 0 dla tego m to mamy tylko jeden pierwiastek tak samo jeżeli f(1) ≥ 0 dla jakiegoś m ∊ R a f(−1) < 0 ale jeżeli f(−1) ≥ 0 i f(1) ≥ 0 to mamy dwa rozwiązania a w poleceniu jest mowa że wystarczy jedno rozwiązanie. Jeżeli f(−1) ≥ 0 dla jakiegoś m ∊ R to t₁ znajduje się pomiędzy [−1 ; 1] ale dla tego m nie jest spełniony warunek f(1) ≥ 0 to t₂ nie znajdzie się w przedziale [−1 ; 1] więc zajdzie sytuacja −1 ≤ t₁ ≤ 1 < t₂ tak samo jeżeli f(1) ≥ 0 dla jakiegoś m ∊ R to t₁ znajduje się pomiędzy [−1 ; 1] ale dla tego m nie jest spełniony warunek f(1) ≥ 0 to t₂ nie znajdzie się w przedziale [−1 ; 1] więc zajdzie sytuacja t₂ < −1 ≤ t₁ ≤ 1 natomiast kiedy f(−1) ≥ 0 dla m ∊ R i dla tego m również zachodzi f(1) to mamy że t₁ oraz t₂ znajduje się w przedziale [−1 ; 1] czyli −1 ≤ t₁ ≤ t₂ ≤ 1. Jak jeszcze coś nie jest jasne napisz postaram się jeszcze lepiej wytłumaczyć.

pigor: ..., no tak, przepraszam, że ci zająłem tyle, czasu, a ja byłem pewien, że chodzi o a) ma rozwiązania, a teraz dopiero przyjrzałem się i jest ma rozwiązanie; jeszcze raz przepraszam za zawracanie głowy . ... P.S. gdybym ja był autorem pytania tak bym nie zapytał, tylko a) ma dokładnie jedno rozwiązanie, ale cóż, to jest życie . ...

ZKS: Ale jak mi zawracasz głowę? Sam chciałem zobaczyć czy dobrze rozumuję to zadanie więc z przyjemnością to tłumaczyłem może się przyda jeszcze komuś to zadanie kiedyś.