Zadanie z planimetrii pulpet112: Na ramionach kąta o wierzchołku A odkładamy dwa odcinki AB i AC, gdzie |AB| = |AC| i dalej kolejne dwa odcinki BD i CE, gdzie |BD| = |CE| . Odcinki BE i DC przecinają się w punkcie O. Wykaż, że prosta AO zawiera dwusieczną kąta BAC. Bardzo proszę o pomoc

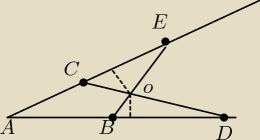
yep: musisz udowodnic przystawanie trojkatow BOD i COE, wtedy ich wysokosci beda rowne, a co za tym idzie − odleglosc punktu O od ramion kata bedzie taka sama

yep: sprobuj, jak cos to pisz

pulpet112: Zgadza sie ale nie bardzo wiem jak udowodnic to ze sa przystajace.... Od razu widac ze jeden kat jest taki sam no i jeden bok ale to za malo zeby stwierdzic przystawanie....

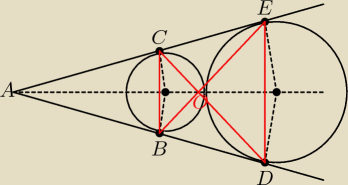
Bogdan: Może ten rysunek będzie przydatny?

pulpet112: Nie wiem, moze mam jakies totalne zacmienie ale nie wiem co ten rysunek wnosi do zadania....

Bogdan: A może dostrzegasz na rysunku trapez równoramienny i jego przekątne?

pulpet112: no tak, dostrzegam ale co w związku z tym?