ostatnie zadanie woj: niech ktos napisze jak rozwiazal ostatnie zadanie za 5 pkt

	336
v=
	t

	336
v+9=
	t−40

dobrze ulozylem uklad rownan?

woj: o maturze ofc mowa

xyz: jak dales t − 40 to juz widze ze zle bo trzeba bylo to na godziny zamienic

Patryk: xyz ile miałeś w tym z ostrosłupem ?

xyz: 400

paulaf: A mógłbyś rozpisać jak zrobiles? XD

Dominik: ja zapisalem vt = 336

	2
(v + 9)(t −		) = 336
	3

po jednym przeksztalceniu dochodzi sie do twojej postaci

	336
v + 9 =
	2   t −   3

niestety jednak miales zla jednostke czasu.

woj: taa, w ostroslupie 400, a co do ukladu to wiedzialem ze zle ulozylem bo delta wychodzila przeogromna i nie dalo sie zpierwiastkowac i sie pogubilem ... coz w plecy 5 pkt

bash: oczywiście założenie powinno być jeszcze v>0

	2
t>
	3

Denar: jeden pociąg 72 km/h, a drugi 63km/h też tak mieliście?

Dominik: tak

anulaa: ^^

anulaa: a nie pierwszy jechał szybciej?

Bogdan: Pokazuję przykładowy zapis zadania z pociągami. v − prędkość I pociągu, v > 0 (v + 9) − prędkość II pociągu, t − liczba godzin jazdy I pociągu na trasie 336 km, t > 0

	2		2
(t −		) − liczba godzin jazdy II pociągu na trasie 336 km, t −		> 0,
	3		3

	2
40 min. =		h
	3

(1) v*t = 336

	2		2
(2) (v + 9)(t −		) = 336 ⇒ 336 −		v + 9t − 6 = 336
	3		3

	2		2		2
(2) 9t =		v + 6 ⇒ t =		v +
	3		27		3

	2		2		27
(1)		v2 +		v − 336 = 0 /*		⇒ v2 + 9v − 4536 = 0
	27		3		2

Δ = 18225, √Δ = 135

	−9 − 135
v =		< 0 sprzeczność
	2

lub

	−9 + 135
v =		= 63 i v + 9 = 72
	2

Odp.: I pociąg jechał z prędkością 63 km/h, II pociąg z prędkością 72 km?/

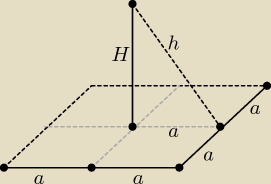
Bogdan: Maturalne zadanie z ostrosłupem można rozwiązać np. tak: P_P = 100 ⇒ 2a = 10 ⇒ a = 5 P_B = 260 ⇒ 4*a*h = 260 ⇒ 4*5*h = 260 ⇒ h = 13 H = √h² − a² = √13² − 5² = 12

	1
Objętość V =		*100 * 12 = 400
	3

Damian: a co jesli nie mam założeń? a poza tym wszystko ok?

Damian: i jeśli w tym zadaniu Bogdanie zrobiłem ok tylko napisałem chyba 400cm² zamiast 400cm³ a punkt?

Damian: to odejmą punkt?

Bogdan: Myślę, że nie odejmą

Bogdan: ale założenia powinny być

anja: Chyba raczej I pociąg jechał 72 km/h, a drugi 63 km/h

Bogdan: W moich oznaczeniach prędkość v jest opisana jako prędkość I pociągu, a (v + 9) jako prędkość II pociągu

maturzystka: Mam pytanie, ja zrobiłam to zadanie tak: V₂ = V₁ − 9 t₂= t₁ + 2/3 Gdzie: V₂ − prędkość wolniejszego pociągu t₂ − czas wolniejszego pociągu V₁ * t₁ = 336 (t₁ + 2/3)(V₁−9)= 336. Wyszło mi 63km/h i 72km/h . Chyba jest to dobry, inny sposób, prawda?

maturzystka: Bogdan, napisałeś że v + 9 to prędkość drugiego, czyli wolniejszego pociągu. Prędkość drugiego pociągu to prędkość pierwszego odjąć 9 a nie plus. Prędkość pierwszego moglibyśmy zapisać jako v+9, ale kiedy v to prędkość drugiego pociągu. Zgadza się?

Karlo: W zadaniu z ostrsłupem brak założenia a>0

Bogdan: Nie napisałem maturzystko, że v+9 to prędkość drugiego, czyli wolniejszego pociągu, ale napisałem, że v+9 to prędkość drugiego pociągu (nie użyłem sformułowania "wolniejszego"), co prawda oznaczyłem pociągi odwrotnie to podanej w treści zadania, gdzie pociąg pierwszy jedzie nie z prędkością v, ale z prędkością v+9. Nie zmienia to jednak sposobu i poprawności rozwiązania, to tak, jakby ktoś zamiast zapisanej w treści zadania literki a określającej długość prostokąta i literki b określającej szerokość przy poleceniu dotyczącym obliczenia pola zamienił oznaczenia i przyjął od samego początku, że b to długość, a a to szerokość. Nie ma sprzeczności w przebiegu przedstawionego przez mnie rozwiązania zadania z pociągami.

Eta: Dla Bogdana ....

maturzystka: Dobrze, tylko po prostu czytając treść zadania, gdzie wyraźnie zaznaczone są pociągi pierwszy i drugi od razu nasuwa się wątpliwość, że oznaczenia są niepoprawne, co nie zmienia faktu że wynik jest dobry, ale po prostu jest to trochę pomieszane. A co z moim tokiem rozumowania i oznaczeniami?

Bogdan: W zadaniu z ostrosłupem Karlo można oczywiście zapisać: a > 0, ale w tym zadaniu nie pojawia się możliwość uzyskania ujemnej wartości a (tak, jak np. w zadaniu z pociągami i tam takie założenie v>0 jest uzasadnione) i zapis a > 0 nie musi pojawić się w treści rozwiązania, tym bardziej, że na rysunku wyraźnie są zaznaczone literką a odcinki w podstawie ostrosłupa, a jak wiemy odcinek nie ma długości ujemnej. Twój maturzystko zapis jest oczywiście poprawny i przedstawia on nie inny, a ten sam sposób rozwiązania zadania, czyli sposób z układem równań, w którym iloczyny pewnych wielkości przyrównane są do stałej wartości. Swoje rozwiązanie przedstawiłem już po egzaminie, ale jeszcze przed opublikowaniem arkuszy maturalnych na podstawie luźnej informacji o dwóch pociągach, z których jeden jechał z prędkością v, a drugi szybciej o 9 km i stąd zapewne przyjąłem takie oznaczenia. Zadania z takim układem od lat występują w arkuszach maturalnych.

Bogdan: Witaj Eto , mamy jednak również wnikliwych maturzystów, co bardzo cieszy

maturzystka: W porządku rozumiem, więc teraz już wszystko jasne Dziękuję bardzo za odpowiedź

Bogdan: Pozdrawiam maturzystko i życzę powodzenia we wszystkich egzaminach, nie tylko maturalnych

maturzystka: Dziękuję i również pozdrawiam

Karlo: możliwośc uzyskania ujemnej "a" pojawia się niestety w tym zadaniu. 100 = (2a)² [(100−(2a²)] = 0 (10−2a)(10+2a) = 0 2a=10 → a=5 2a = −10 → a=−5 Gdy nie napiszemy odpowiedniego założenia, nasze zadanie legnie w gruzach.. Pozdrawiam

pigor: ..., a ja zawsze rozwiązywałem sobie takie zadania równaniem np. tak: niech v+9, v= ? − szukane prędkości średnie 1−szego i 2−ego pociągu odpowiednio i v >0, to z warunków zadania i znajomości nieco fizyki : t₁ =t₂−40'= t₂−⁴⁰₆₀= t₂−²₃ ⇔ ⇔ ³³⁶_v+9= ³³⁶_v − ²₃ / * ³₂v(v+9) ⇔ 504v= 504v+ 504*9− v(v+9) ⇔ ⇔ v²+9v−504*9= 0 i Δ=9²+4*504*9= 9²+ 4*56*9²= 9²*225, więc √Δ= 9*15= 135, ⇒ v= ¹₂(−9+135)= ¹₂*126 = 63 >0 , oraz v+9= 63+9= 72, zatem odp. 72^km_h i 63 ^km_h − szukane prędkości średnie pociągów . ...