 zad 1.
Wiadomo, że α jest kątem ostrym i tg α + ctg α = 4 Oblicz √tg2α+ctg2α
wskazówka: ctg α = 1tg α
zad 2.
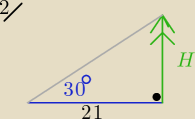
Drzewo rzuca cień długości 21 m. Oblicz wysokość drzewa wiedząc że promienie słoneczne padają
na płaszczyznę poziomą pod kątem 30o Wynik podaj z dokładnością do 1 metra
Zad 3.
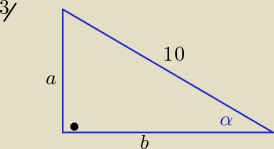
W trójkącie prostokątnym sinus jednego z kątów ostrych ma wartość 45 Oblicz długość
przyprostokątnej tego trójkąta wiedząc że przeciwprostokątna ma długość 10cm
Zad 4.
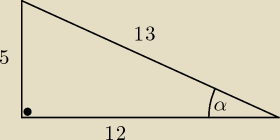
Boki trójkąta prostokątnego mają długość 5, 12, 13. Jaką wartość przyjmuje | sin α − cos α|
jeżeli α jest najmnijeszym kątem w tym trójkącie
zad 5.
Uzasadnij, że nie istnieje kąt ostry α taki, że:
sin α + cos α = 53
zad 6.
Wiedząc, że α jest kątem ostrym i sin α = 14 oblicz:
sin α * cos α
zad 7.
Długość boku równoległoboku jest o 3 większa od wysokości opuszczonej na ten bok. Wyznacz
długości boków równoległoboku wiedząc, że jego pole jest równe 10 i sin α = 34, gdzie α
jest kątem ostrym równoległoboku.
zad 1.
Wiadomo, że α jest kątem ostrym i tg α + ctg α = 4 Oblicz √tg2α+ctg2α
wskazówka: ctg α = 1tg α
zad 2.
Drzewo rzuca cień długości 21 m. Oblicz wysokość drzewa wiedząc że promienie słoneczne padają
na płaszczyznę poziomą pod kątem 30o Wynik podaj z dokładnością do 1 metra
Zad 3.
W trójkącie prostokątnym sinus jednego z kątów ostrych ma wartość 45 Oblicz długość
przyprostokątnej tego trójkąta wiedząc że przeciwprostokątna ma długość 10cm
Zad 4.
Boki trójkąta prostokątnego mają długość 5, 12, 13. Jaką wartość przyjmuje | sin α − cos α|
jeżeli α jest najmnijeszym kątem w tym trójkącie
zad 5.
Uzasadnij, że nie istnieje kąt ostry α taki, że:
sin α + cos α = 53
zad 6.
Wiedząc, że α jest kątem ostrym i sin α = 14 oblicz:
sin α * cos α
zad 7.
Długość boku równoległoboku jest o 3 większa od wysokości opuszczonej na ten bok. Wyznacz
długości boków równoległoboku wiedząc, że jego pole jest równe 10 i sin α = 34, gdzie α
jest kątem ostrym równoległoboku.

 Rozwiążę Ci ( wzrośnie nam w kraju wskaźnik wykształconych obywateli
Rozwiążę Ci ( wzrośnie nam w kraju wskaźnik wykształconych obywateli  1/ tgα+ctgα=4 /2
tg2α+2tgα*ctgα+ctg2α= 16
tg2α+ctg2α+2*1=16
tg2α+ctg2α= 14
√tg2α+ctg2α=√14
2/
1/ tgα+ctgα=4 /2
tg2α+2tgα*ctgα+ctg2α= 16
tg2α+ctg2α+2*1=16
tg2α+ctg2α= 14
√tg2α+ctg2α=√14
2/
| H | √3 | |||
= tg30o , tg30o= | ||||
| 21 | 3 |
| H | √3 | |||
= | ||||
| 21 | 3 |
| 21√3 | ||
H= | = 7√3≈ 7*1,73 = 12 m | |
| 3 |

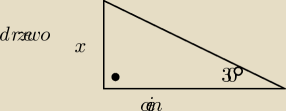 zad 2. cos 30 = 21x oblicz
zad 2. cos 30 = 21x oblicz
| 1 | ||
√tg2 α +ctg2 α = √(tg α +ctg α)2 − 2tgαctgα = √16 − 2tgα x | = √16 − 2 = | |
| tgα |
 3/
a,b>0
3/
a,b>0
| a | 4 | 40 | ||||
sinα= | = | ⇒ a= | = 8 cm | |||
| 10 | 5 | 5 |

 ?
?
 4.
4.
| 5 | ||
sinα= | ||
| 13 |
| 12 | ||
cosα= | ||
| 13 |
| 5 | 12 | 7 | 7 | |||||
|sinα−cosα|=| | − | |=|− | |= | |||||
| 13 | 13 | 13 | 13 |
| 5 | ||
załóżmy, że sinα+cosα= | i α kąt ostry | |
| 3 |
| 25 | ||
(sinα+cosα)2= | ||
| 9 |
| 25 | ||
sin2α+2sinαcosα+cos2α= | ||
| 9 |
| 25 | ||
1+2sinαcosα= | ||
| 9 |
| 25 | ||
2sinαcosα= | −1 | |
| 9 |
| 16 | ||
sin2α= | ||
| 9 |
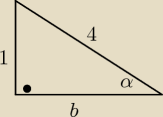 6.
obliczam długość drugiej przyprostokątnej z tw. Pitagorasa:
12+b2=42
b2=16−1
b=√15
6.
obliczam długość drugiej przyprostokątnej z tw. Pitagorasa:
12+b2=42
b2=16−1
b=√15
| √15 | ||
cosα= | ||
| 4 |
| 1 | √15 | √15 | ||||
sinα*cosα= | * | = | ||||
| 4 | 4 | 16 |
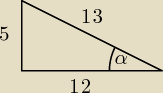 4)
Najdłuższym bokiem trójkąta prostokątnego jest zawsze przeciwprostokątna, najmniejszy ką leży
naprzeciw najkrótszego boku.
4)
Najdłuższym bokiem trójkąta prostokątnego jest zawsze przeciwprostokątna, najmniejszy ką leży
naprzeciw najkrótszego boku.
| przyprostokątna naprzeciw kąta α | ||
Sinus α to stosunek | ||
| przeciwprostokątna |
| 5 | ||
sinα= | ||
| 13 |
| przyprostokątna przy kącie α | ||
Cosinus α to stosunek | ||
| przeciwprostokątna |
| 12 | ||
cosα= | ||
| 13 |
| 5 | 12 | −7 | 7 | |||||
| | − | |=| | |= | |||||
| 13 | 13 | 13 | 13 |
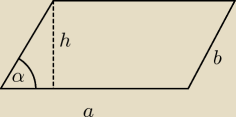 7.
7.
| 3 | ||
sinα= | ||
| 4 |
| −b−√Δ | −3−7 | |||
h1= | = | =−5 − nie może być ujemne bo to długość odcinka | ||
| 2a | 2 |
| −b+√Δ | −3+7 | |||
h2= | = | =2 − ok | ||
| 2a | 2 |
| 3 | ||
inny wzór na pole: P=a*b*sinα, stąd 10=5*b* | ||
| 4 |
| 4 | 8 | |||
b=2* | = | |||
| 3 | 3 |

 P=x*3x=3x2 =10
P=x*3x=3x2 =10
| 3 | x | |||
sinα= | = | |||
| 4 | a |
| 10 | ||
x2= | ||
| 3 |
| √10 | ||
x= | ||
| √3 |
| 3√10 | ||
3x= | − pierwszy bok | |
| √3 |
| 3 | x | ||
= | |||
| 4 | a |
| 3 |
| ||||||||
= | |||||||||
| 4 | a |
| 3 | √10 | ||
= | |||
| 4 | a√3 |
| 4√10 | √3 | |||
a= | /* | |||
| 3√3 | √3 |
| 4√30 | ||
a= | ||
| 9 |

 całe zadanie do kosza
całe zadanie do kosza 