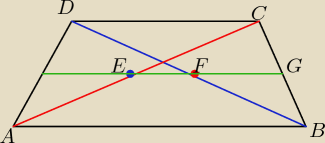
 W trapezie o podstawach a, b gdzie a,b>0. Wykaż ze długość odcinaka łączącego środki
W trapezie o podstawach a, b gdzie a,b>0. Wykaż ze długość odcinaka łączącego środki
| a−b | ||
przekątnych jest równa | ||
| 2 |
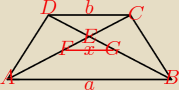 ja zrobilabym to tak
trójkąty ABE i FGE oraz ECD są podobne na podstawie cechy kk
więc a/|AE|=x/||FE|=b/|CE|
AE=1/2|AC|+|FE|
FC=1/2|AC|−|FE|
układ równań z : a/1/2|AC|+|FE|=x/|FE|
x/|FE|=b/1/2|AC|−|FE|
wymnazam na krzyż.
1/2|AC|x+|FE|x=|FE|a
1/2|AC|x−|FE|x=|FE|b
podstawiam 1/2|AC|x z pierwszego do drugiego :
|FE|a−|FE|x−|FE|x=|FE|b pozbywam sie |FE|
a−x−x=b
a−b=2x
x=a−b/2
ja zrobilabym to tak
trójkąty ABE i FGE oraz ECD są podobne na podstawie cechy kk
więc a/|AE|=x/||FE|=b/|CE|
AE=1/2|AC|+|FE|
FC=1/2|AC|−|FE|
układ równań z : a/1/2|AC|+|FE|=x/|FE|
x/|FE|=b/1/2|AC|−|FE|
wymnazam na krzyż.
1/2|AC|x+|FE|x=|FE|a
1/2|AC|x−|FE|x=|FE|b
podstawiam 1/2|AC|x z pierwszego do drugiego :
|FE|a−|FE|x−|FE|x=|FE|b pozbywam sie |FE|
a−x−x=b
a−b=2x
x=a−b/2