Geometria analityczna Geometria analityczna: Napisz równanie prostej zawierającej wysokość poprowadzoną z wierzchołka C w trójkącie ABC, gdzie A(−2,−1) B(4,2), C(0,5).

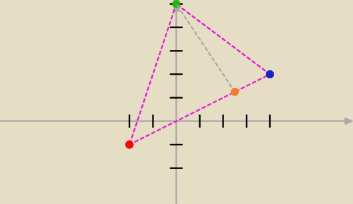
Alicja: Narysujmy trójkąt w układzie współrzędnych, gdzie punkt: A − czerwony B − niebieski C − zielony D − pomarańczowy Zakładamy że punkt D jest miejscem gdzie wysokość c przetnie odcinek AB Wiemy że równanie prostej to y=a_kx+b_k oraz znamy jeden punkt należącej do tej prostej C(0,5) oraz wiemy że prosta ma być prostopadła do prostej przechodzącej przez odcinek AB. k − prosta której równanie mamy obliczyć l − prosta przechodząca przez punkt A i B Obliczam równanie prostej l: y=a_lx+b_l

⎧	−1=−2al+bl ⇒ bl=2al−1
⎩	2=4al+bl

2=4a_l+2a_l−1 6a_l=3 a_l=¹₃ Wiemy że a_k=−¹_al ⇒a_k = −3 Więc równanie prostej k to y=−3x+b_k w wykresu wyczytujemy b_k (jak ktoś chce może obliczyć lecz poco xD) b_k=5 i oto wzór końcowy k:y=−3x+5

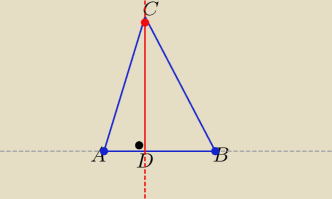Eta: prosta AB ⊥ prostej CD

	2+1		1
aAB=		=		, to aCD= −2
	4+2		2

pr. CD: y= −2(x−x_C)+y_C y= −2x+5