planimetria
monia: w trójkącie przyprostokątnym ABC przyprostokątne maja długości 5 i 12.Z wierzchołka A
zakreślono łuk o promieniu 12,a z wierzchołka B luk o promieniu 5 i otrzymano punkty E i
D.Oblicz długość odcinka ED.
15 wrz 21:55
Bogdan:
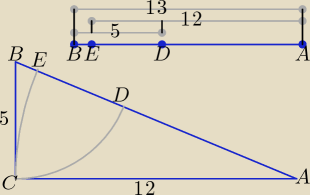
Z twierdzenia Pitagorasa w trójkącie ABC otrzymujemy |AB| = 13
Odcinek ED jest wspólną częścią odcinka BD i EA
|AB| = |BD| + |EA| − |ED| ⇒ |ED| = |BD| + |EA| − |AB| ⇒ |ED| = 5 + 12 − 13 = 4
16 wrz 00:32
AROB:
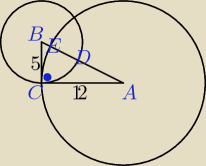
/ED/ = ?
/AB/ = 13 (z tw. Pitagorasa)
/AD/ =/AB/ −/BD/ = 13 − 5 = 8
/BE/= /AB/ − /AE/ = 13 − 12 = 1
/ED/ = /AB/ − (/AD/ + /BE/ ) = 13 − (8 + 1) = 13 − 9 =
4
16 wrz 00:36
Eta:
16 wrz 00:40
AROB: 
16 wrz 00:41
Eta:
Idę już do
Dobranoc Wszystkim
16 wrz 00:43
AROB: Dobranoc
Eta i
Bogdanie. Też idę do
16 wrz 00:47
Bogdan:
Dobranoc
16 wrz 00:53