Ciągi i geometria - 2 LO Aru: Nie mam pojęcia czy takie zadania już tutaj były, ale nie mogę ich znaleźć. Byłabym wdzięczna za wskazówki : ) 1. Wykaż, że jeśli d₁, d₂ są długościami przekątnych równoległoboku o bokach długości a, b i kącie ostrym α = 60°, przy czym d₁ < d₂, to d₂² −d₁² = 2ab. 2. Wyznacz te wartości x, dla których ciąg geometryczny 3−x, (3−x)²/2 , (3−x)³/4 , (3−x)⁴/8 , ... jest zbieżny. Wyznacz zbiór wartości funkcji f(x) = 3−x, (3−x)²/2 + (3−x)³/4 + (3−x)⁴/8 , ... 3. Długości cięciw AB, BC i CD są równe, |∠E| = 20°. a) Oblicz miarę kąta ACD. b) Oblicz długość odcinka AC, jeśli |CE| = 6. Wynik zaokrąglij do części dziesiątych. http://imageshack.us/a/img853/6628/matdl.png

aniabb: 1. twierdzenie cosinusów 2. zbieżny jak |q|<1 więc |(3−x)/2|<1 więc 1<x<5

Aru: Dziękuję. Problem w tym, że ni w ząb nie rozumiem tych twierdzeń (nie wspominając, że nawet ich nie miałam...) :<

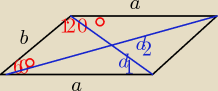
aniabb: d₂²= a²+b²−2abcos120° = a²+b²+ab d₁²= a²+b²−2abcos60° = a²+b²−ab −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−odejmujemy stronami d₂²−d₁² = ab−(−ab) = 2ab

Aru: Wielkie dzięki <3 A wiesz może jak to z kołem zrobić?

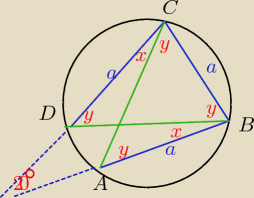
aniabb: już wiem ..na świeżo nowy pomysł kąt ACD =x = kąt DBA bo wpisane na tym samym łuku kąt CDB =y = kąt BAC bo wpisane na tym samym łuku kąt BAC = kąt ACB bo trójkąt ABC równoramienny kąt CDB = kąt CBD bo trójkąt DBC równoramienny 20°+x+y+x+y=180° więc x+y=80° x+y+y+y=180° 80+2y=180 y=50° x=30° Odp kąt ACD=30°

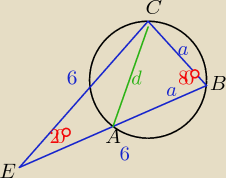
aniabb: tw cosinusów trójkąt EBC a²=6²+6²−2•6•6•cos20° = 72−72•0,93969 = 4,34213130 a=2,083778132 tw cosinusów trójkąt ABC d²=a²+a²−2•a•a•cos80° = 2•4,34213130 −2•4,34213130•0,17364 = 7,176256230 d= 2,678853 ≈ 2,7

Aru: Stokrotne dzięki! ! ! Nie wiem jak się odwdzięczę, ale dziękuję : D (Teraz nawet jestem w stanie to zrozumieć, haha ).