oblicz wartość parametru. KASIA: Dla jakich wartości parametru m nierówność mx² − 4x + m +3 ≥ 0 będzie spełniona dla każdej liczby rzeczywistej x?

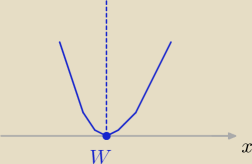
Eta: Witam: by spełniony był warunek zadania , to parabola musi być : ramionami zwrócona do góry zatem: a>0 i wierzchołek musi należeć do osi OX , więc Δ= 0 zatem parametr "m" musi spełniać układ warunków: 1/ a> 0 => m >0 i 2/ Δ=0 => 16 − 4*m( m+3) =0 to: 4m² +12m −16 =0 /:4 m² +3m −4 =0 rozwiąz to równanie i jako odp. podaj to "m" ,które jest >0 i to wszystko

KASIA: ale to bedzie wynik dla funkcji rownej 0 a tam jest ze jest większa lub równa.. wiec co z tym jak będzie większa?

KASIA: czyli trzeba z tego zrobić przedział, tak? i z tego przedziały wybrać jeszcze ten przedział który należy do (0; +∞) tak? wyszło mi że od <1; +∞) .

Mattaii: Mi tak samo wyszło więc jest małe prawdopodobieństwo abyśmy mieli źle ; D

KASIA: ciesze się niezmiernie i dziękuję bardzo za pomoc