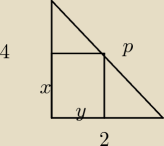
 1.W trójkącie równoramiennym jest wpisany prostokąt (rysunek). podaj wymiary tego prostokąta
tak aby jego pole było największe a także podaj wymiary żeby było najmniejsze. Długość
przyprostkatnych tego trojkata ma dlugosc 4 a przeciwprostokatna 4√2.
czy mogłabym liczyć na pomoc
1.W trójkącie równoramiennym jest wpisany prostokąt (rysunek). podaj wymiary tego prostokąta
tak aby jego pole było największe a także podaj wymiary żeby było najmniejsze. Długość
przyprostkatnych tego trojkata ma dlugosc 4 a przeciwprostokatna 4√2.
czy mogłabym liczyć na pomoc 
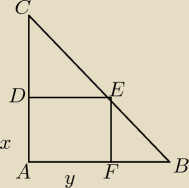 jeśli chcemy aby pole było najmniejsze to automatycznie pole dwóch trójkątów musi być
największe. uzależnimy oba pola od jednej zmiennej i poszukamy wartości maksymalnej funkcji
którą otrzymamy. Propoznuje skożystać z podobieństwa trójkątów powołując sie na ceche kąt kąt
jeśli chcemy aby pole było najmniejsze to automatycznie pole dwóch trójkątów musi być
największe. uzależnimy oba pola od jednej zmiennej i poszukamy wartości maksymalnej funkcji
którą otrzymamy. Propoznuje skożystać z podobieństwa trójkątów powołując sie na ceche kąt kąt
| CD | DE | 4−x | y | ||||
= | ==> | = | ==> y=4−x | ||||
| EF | FB | x | 4−y |
| 1 | ||
PCDE= | *4−x*4−x | |
| 2 |
| 1 | ||
PEFB= | *x*x | |
| 2 |