Oblicz długość odcinka podanego w treści zadania Szymek: Trapez równoramienny o dłuższej podstawie równej 11 i o bokach równych 5, którego dwusieczne przecinają kąty przy dłuższej podstawie został przedzielony odcinkiem łączącym środki boków trapezu. Oblicz długość tego odcinka

Szymek: Nikt nie pomoże?

Bogdan: To może sam wykonasz chociaż rysunek i oznaczysz go, co?

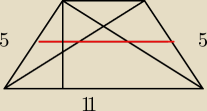
Szymek: Proszę bardzo czekałem tylko aż ktoś się odezwie. Próbowałem już kombinować z tw. cosinusów układ z tego albo podobieństwa.

Szymek: Wiem, że brakuje kątów i oznaczenia drugiej podstawy ale pierwszy raz zadaje tu pytanie i nie wszystko jeszcze ogarnąłem

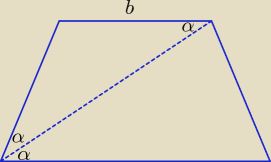
Bogdan: Spróbuj wyznaczyć b − długość krótszej podstawy

Szymek: skoro są takie same katy przy podstawie to b=5?

Bogdan:

	a + b
odcinki a, e, b są równoległe, e =
	2

Szymek: jesli tak zrobie to wyjdzie prawidlowo bo srednia arytmetyczna podstaw da mi szukany odcinek

Bogdan:

Szymek: nie wiedzialem tylko ze mozna tak oznaczyc te katy. Wiedzialem ze na podstawie nie moze byc za wiele kombinacji jednak gdy sie robi caly czas rozszerzenia to potem na prosty zadaniu idzie sie zlapac

Szymek: Dziekuję Ci bardzo Bogdanie rozwiałeś moje niespokojne myśli

Bogdan: No, bez przesady z tymi niespokojnymi myślami, pozdrawiam