Dowód Kejt: Mógłby ktoś podpowiedzieć jak wykazać wzór na pole czworokąta, z danymi przekątnymi i kątem między nimi?

	1
P=		cdsinα
	2

Proszę tylko o drobną podpowiedź..

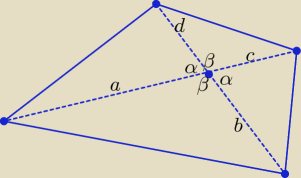
Bogdan: β = 180^o − α, sinβ = sinα przekątne: e = a + c, f = b + d,

	1		1		1		1
pole czworokąta P =		absinβ +		bcsinα +		cdsinβ +		adsinα = ...
	2		2		2		2

Kejt: dziękuję Bogdanie idę spać..mam dosyć..

Bogdan: Tak wcześnie spać?

Kejt: mój biedny mózg przestał pracować..nie dam rady dziś zrobić ani jednego zadania więcej..

Bogdan: ale można sobotni wieczór spędzać równie przyjemnie nie rozwiązując zadań

Tomek: masz racje Bogdan zawsze można przeciez poczytać streszczenia lektur do matury....

Krzysiek : Tomek. Nasza Biedna Kejt ma sie odprezyc tzn, isc na impreze i a nie czytac lektury

Tomek: też bym tak chciał ale mature ma sie raz... no chociaz nie koniecznie... ale tego nie chce wiec siedze w sobotni wieczór i czytam streszczenia... po prostu żyć nie umierac...

amenstia:

	1
ale nie wiem jak to dalej, mi wychodzi np.		sinβ(be+df)
	2

amenstia: ?

Kejt: o dziwo wczoraj prawie to skończyłam to będzie tak:

	1		1		1		1
P=		sinα(bc+ad)+		sinβ(ab+cd)=		sinα(bc+ad)+		sin(180o−α)(ab+cd)=
	2		2		2		2

1		1		1		1
	sinα(bc+ad)+		sinα(ab+cd)=		sinα(bc+ad+ab+cd)=		sinα(a+c)(b+d)
2		2		2		2